Zadanie nr 8910387
Granica 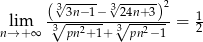 . Wynika stąd, że
. Wynika stąd, że
A) 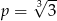 B)
B) 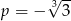 C)
C) 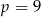 D)
D) 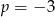
Rozwiązanie
Liczymy granicę nie przejmując się parametrem – dzielimy licznik i mianownik przez 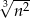 .
.
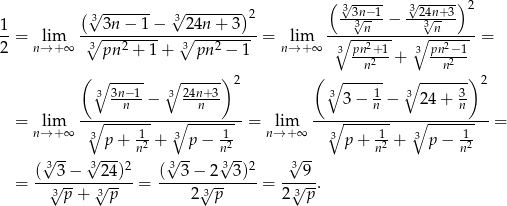
Stąd
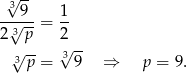
Odpowiedź: C
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Granica 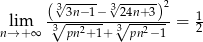 . Wynika stąd, że
. Wynika stąd, że
A) 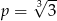 B)
B) 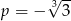 C)
C) 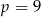 D)
D) 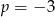
Liczymy granicę nie przejmując się parametrem – dzielimy licznik i mianownik przez 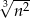 .
.
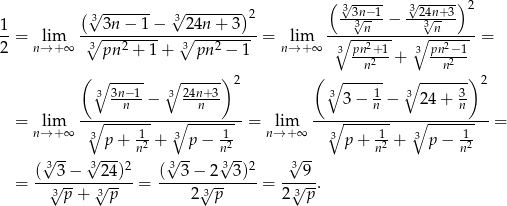
Stąd
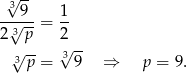
Odpowiedź: C
