/Szkoła średnia/Zadania testowe/Ciągi/Granice

Zadanie nr 8924530

Granica

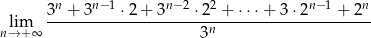
n n− 1 n− 2 2 n−1 n lim 3--+-3----⋅2-+-3----⋅2--+-⋅⋅⋅+--3⋅-2----+-2-- n→+ ∞ 3n

jest równa
A) 2 B) 3 C) 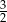32 D) 0

Wersja PDF

Rozwiązanie

Jeżeli daną granicę zapiszemy w postaci

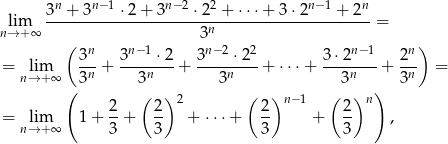
n n−1 n− 2 2 n−1 n lim 3--+-3----⋅2-+-3----⋅2--+-⋅⋅⋅+--3⋅2----+--2--= n→ + ∞ ( 3n ) 3n 3n−1 ⋅2 3n −2 ⋅ 22 3⋅2n− 1 2n = lim --n + ----n---+ -----n---+ ⋅⋅⋅+ ---n----+ -n- = n→ + ∞( 3 3( ) 3 ( ) ( 3 ) ) 3 2 2 2 2 n− 1 2 n = lim 1 + --+ -- + ⋅ ⋅⋅+ -- + -- , n→ + ∞ 3 3 3 3

to widać, ze musimy obliczyć sumę szeregu geometrycznego o pierwszym wyrazie 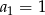a1 = 1 i ilorazie 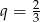2 q = 3 . Suma ta jest równa

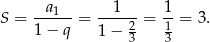
a1 1 1 S = ------= ----2-= 1-= 3. 1 − q 1 − 3 3

 
Odpowiedź: B

Wersja PDF