/Szkoła średnia/Zadania maturalne/Matura 2016/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 5 marca 2016 Czas pracy: 170 minut
Zadania zamknięte
Liczba 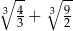 jest równa
jest równa
A) 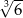 B)
B) 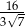 C)
C) 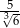 D)
D) 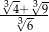
Dane są liczby 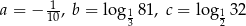 . Iloczyn
. Iloczyn 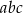 jest równy
jest równy
A) 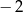 B)
B) 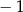 C)
C) 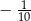 D)
D) 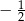
Dany jest prostopadłościan o wymiarach 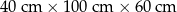 . Jeżeli każdą z najdłuższych krawędzi tego prostopadłościanu wydłużymy o 30%, a każdą z najkrótszych krawędzi skrócimy o 20%, to w wyniku obu tych przekształceń objętość tego prostopadłościanu
. Jeżeli każdą z najdłuższych krawędzi tego prostopadłościanu wydłużymy o 30%, a każdą z najkrótszych krawędzi skrócimy o 20%, to w wyniku obu tych przekształceń objętość tego prostopadłościanu
A) zwiększy się o 8% B) zwiększy się o 4%
C) zmniejszy się o 8% D) zmniejszy się o 4%
Liczby 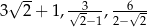 są kolejnymi wyrazami ciągu
są kolejnymi wyrazami ciągu
A) arytmetycznego B) geometrycznego C) rosnącego D) malejącego
Para liczb 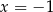 i
i 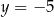 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 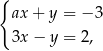 gdy
gdy
A) 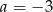 B)
B) 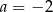 C)
C) 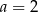 D)
D) 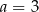
Rozwiązaniem równania 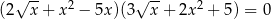 jest liczba
jest liczba
A) 1 B) 2 C) 4 D) 9
Wartość wyrażenia 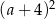 jest większa od wartości wyrażenia
jest większa od wartości wyrażenia 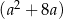 o
o
A) 4 B) 16 C) 64 D) 8
Najmniejszą liczbą całkowitą spełniającą nierówność 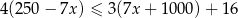 jest
jest
A) 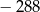 B)
B) 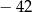 C)
C) 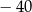 D)
D) 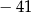
Na rysunku przedstawiony jest fragment prostej o równaniu 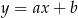 przechodzącej przez punkty
przechodzącej przez punkty 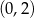 i
i 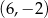 .
.
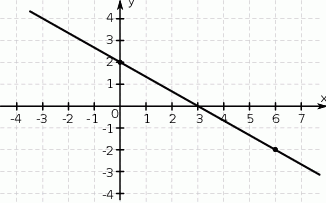
Wtedy
A) 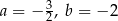 B)
B) 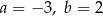 C)
C) 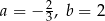 D)
D) 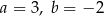
Przez wierzchołek 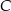 trójkąta prostokątnego
trójkąta prostokątnego 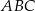 poprowadzono styczną do okręgu opisanego na tym trójkącie.
poprowadzono styczną do okręgu opisanego na tym trójkącie.
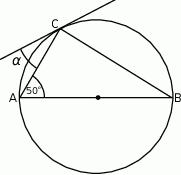
Jeżeli 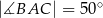 to miara kąta
to miara kąta  jest równa
jest równa
A) 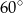 B)
B) 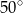 C)
C) 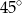 D)
D) 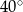
Funkcja kwadratowa określona jest wzorem 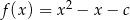 . Jeżeli
. Jeżeli 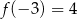 , to
, to
A) 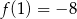 B)
B) 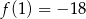 C)
C) 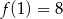 D)
D) 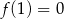
Na rysunku przedstawiono wykres funkcji 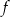 .
.
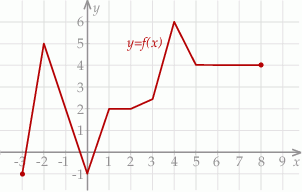
Najdłuższy przedział, na którym funkcja 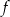 jest rosnąca to
jest rosnąca to
A) 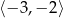 B)
B) 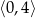 C)
C) 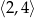 D)
D) 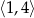
Wykres funkcji liniowej 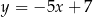 przecina pionową prostą przechodzącą przez punkt
przecina pionową prostą przechodzącą przez punkt 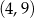 w punkcie o współrzędnych
w punkcie o współrzędnych
A) 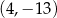 B)
B) 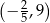 C)
C) 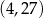 D)
D) 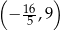
W ciągu geometrycznym 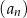 dane są:
dane są: 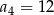 i
i 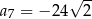 . Iloraz ciągu
. Iloraz ciągu 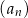 jest równy
jest równy
A) 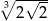 B)
B) 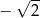 C)
C) 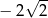 D)
D) 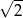
Jeżeli 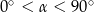 oraz
oraz 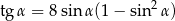 , to
, to
A) 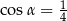 B)
B) 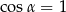 C)
C) 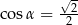 D)
D) 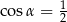
Miary kątów wewnętrznych pewnego trójkąta pozostają w stosunku 2:4:9. Największy kąt wewnętrzny tego trójkąta ma miarę
A) 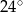 B)
B) 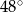 C)
C) 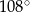 D)
D) 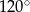
Kąt  jest najmniejszym z kątów trójkąta prostokątnego o bokach długości
jest najmniejszym z kątów trójkąta prostokątnego o bokach długości 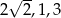 . Wtedy
. Wtedy
A) 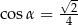 B)
B) 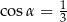 C)
C) 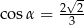 D)
D) 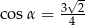
W kwadracie 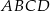 połączono środki boków otrzymując kwadrat
połączono środki boków otrzymując kwadrat 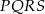 .
.
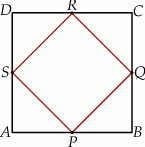
Kwadrat 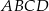 jest podobny do kwadratu
jest podobny do kwadratu 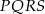 w skali
w skali
A) 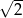 B) 2 C)
B) 2 C) 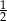 D)
D) 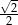
Proste o równaniach: 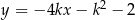 oraz
oraz 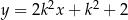 są prostopadłe dla
są prostopadłe dla
A) 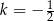 B)
B) 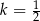 C)
C)  D)
D) 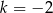
Trójkąt prostokątny 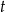 obrócono względem dłuższej przyprostokątnej i otrzymano stożek o polu powierzchni bocznej
obrócono względem dłuższej przyprostokątnej i otrzymano stożek o polu powierzchni bocznej 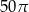 i kącie rozwarcia
i kącie rozwarcia 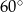 . Obwód trójkąta
. Obwód trójkąta 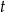 jest równy
jest równy
A) 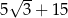 B)
B) 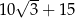 C)
C) 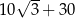 D)
D) 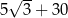
W grupie jest 15 kobiet i 18 mężczyzn. Losujemy jedną osobę z tej grupy. Prawdopodobieństwo tego, że będzie to mężczyzna, jest równe
A) 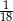 B)
B) 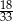 C)
C) 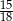 D)
D) 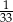
Liczba 0,2 jest jednym z przybliżeń liczby 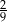 . Błąd względny tego przybliżenia, wyrażony w procentach, jest równy
. Błąd względny tego przybliżenia, wyrażony w procentach, jest równy
A) 1% B) 10% C) 2,2% D) 22%
W ostrosłupie prawidłowym czworokątnym wszystkie krawędzie mają jednakową długość, a pole powierzchni całkowitej tego ostrosłupa jest równe 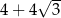 . Wobec tego długość wysokości tego ostrosłupa jest równa
. Wobec tego długość wysokości tego ostrosłupa jest równa
A) 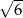 B) 2 C)
B) 2 C) 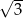 D)
D) 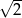
Zadania otwarte
Rozwiąż nierówność 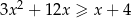 .
.
Rozwiąż równanie 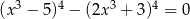 .
.
Mamy trzy pudełka: w pierwszym znajduje się 6 kul ponumerowanych kolejnymi liczbami od 1 do 6, w drugim – 4 kule ponumerowane kolejnymi liczbami od 1 do 4, a w trzecim – 5 kul ponumerowanych kolejnymi liczbami od 1 do 5. Losujemy po jednej kuli z każdego pudełka i tworzymy liczbę trzycyfrową w ten sposób, że numer kuli wylosowanej z pierwszego pudełka jest cyfrą setek, numer kuli wylosowanej z drugiego pudełka jest cyfrą dziesiątek, a numer kuli wylosowanej z trzeciego – cyfrą jedności tej liczby. Oblicz prawdopodobieństwo, że utworzona liczba jest podzielna przez 4.
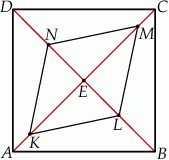
Dany jest kwadrat 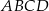 . Przekątne
. Przekątne 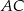 i
i 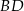 przecinają się w punkcie
przecinają się w punkcie 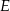 . Punkty
. Punkty 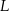 i
i 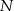 są środkami odcinków – odpowiednio –
są środkami odcinków – odpowiednio – 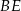 i
i 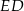 . Punkty
. Punkty 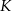 i
i 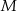 leżą na przekątnej
leżą na przekątnej 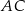 tak, że
tak, że 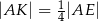 i
i 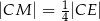 (zobacz rysunek). Wykaż, że stosunek pola czworokąta
(zobacz rysunek). Wykaż, że stosunek pola czworokąta 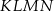 do pola kwadratu
do pola kwadratu  jest równy 3:8.
jest równy 3:8.
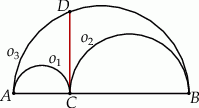
Na średnicy  półokręgu
półokręgu  wybrano punkt
wybrano punkt 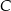 i na odcinkach
i na odcinkach 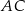 i
i 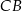 jako na średnicach skonstruowano półokręgi
jako na średnicach skonstruowano półokręgi 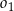 i
i 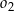 . Odcinek
. Odcinek 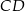 jest odcinkiem wspólnej stycznej półokręgów
jest odcinkiem wspólnej stycznej półokręgów 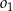 i
i 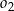 . Oblicz długość odcinka
. Oblicz długość odcinka 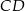 jeżeli promienie półokręgów
jeżeli promienie półokręgów 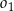 i
i 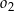 są odpowiednio równe
są odpowiednio równe 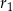 i
i 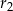 .
.
Wykaż, że dla dowolnych dodatnich liczb rzeczywistych 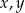 prawdziwa jest nierówność
prawdziwa jest nierówność 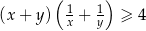 .
.
Dany jest dodatni ułamek nieskracalny. Jeżeli dodamy do licznika ułamka 20% mianownika, a następnie od mianownika odejmiemy 20% zmienionego licznika, to otrzymamy 1,25. Jeżeli natomiast do mianownika danego ułamka dodamy 25% licznika, a od licznika odejmiemy 1, to otrzymamy 0,5. Wyznacz ten ułamek.
Boki 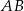 i
i 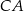 trójkąta
trójkąta 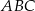 są zawarte w prostych
są zawarte w prostych 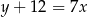 i
i 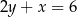 , a jego dwa wierzchołki mają współrzędne
, a jego dwa wierzchołki mają współrzędne 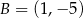 i
i 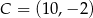 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
W nieskończonym rosnącym ciągu geometrycznym 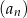 o wyrazach dodatnich, określonym dla
o wyrazach dodatnich, określonym dla 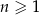 , stosunek średniej geometrycznej trzech pierwszych wyrazów do średniej arytmetycznej tych wyrazów jest równy
, stosunek średniej geometrycznej trzech pierwszych wyrazów do średniej arytmetycznej tych wyrazów jest równy 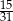 , a suma czterech pierwszych wyrazów tego ciągu jest równa 468. Wyrazy
, a suma czterech pierwszych wyrazów tego ciągu jest równa 468. Wyrazy 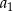 i
i 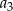 ciągu
ciągu 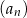 , są odpowiednio pierwszym i trzecim wyrazem ciągu arytmetycznego
, są odpowiednio pierwszym i trzecim wyrazem ciągu arytmetycznego 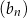 . Oblicz sumę 10 początkowych wyrazów ciągu
. Oblicz sumę 10 początkowych wyrazów ciągu 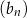 .
.
Uwaga: średnia geometryczna liczb 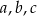 jest równa
jest równa 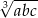 .
.
Objętość ostrosłupa prawidłowego trójkątnego 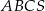 jest równa
jest równa 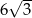 , a krawędź boczna tworzy z płaszczyzną podstawy kąt
, a krawędź boczna tworzy z płaszczyzną podstawy kąt 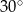 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.

