/Szkoła średnia/Zadania maturalne/Matura 2016/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 9 kwietnia 2016 Czas pracy: 170 minut
Zadania zamknięte
Liczba  jest równa
jest równa
A) 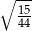 B)
B) 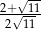 C) 1 D)
C) 1 D) 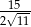
Dane są liczby 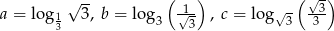 . Iloczyn
. Iloczyn 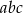 jest równy
jest równy
A) 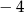 B)
B) 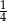 C)
C) 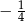 D) 4
D) 4
Dany jest prostokąt o wymiarach 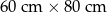 . Jeżeli każdy z dłuższych boków tego prostokąta wydłużymy o 10%, a każdy z krótszych boków skrócimy o 10%, to w wyniku obu przekształceń pole tego prostokąta
. Jeżeli każdy z dłuższych boków tego prostokąta wydłużymy o 10%, a każdy z krótszych boków skrócimy o 10%, to w wyniku obu przekształceń pole tego prostokąta
A) zwiększy się o 2%
B) zwiększy się o 1%
C) zmniejszy się o 1%
D) zmniejszy się o 2%
Po wymnożeniu wyrażeń 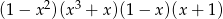 najwyższa potęga
najwyższa potęga  jaką otrzymamy to
jaką otrzymamy to
A) 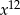 B)
B) 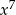 C)
C) 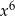 D)
D) 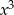
Trójka liczb 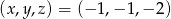 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 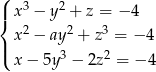 gdy
gdy
A) 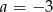 B)
B) 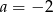 C)
C) 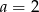 D)
D) 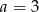
Suma wszystkich pierwiastków równania 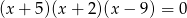 jest równa
jest równa
A) 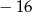 B) 2 C) 16 D)
B) 2 C) 16 D) 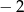
Liczba 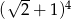 jest większa od liczby
jest większa od liczby 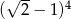 o
o
A) 2 B) 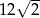 C)
C) 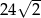 D)
D) 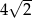
Najmniejszą liczbą całkowitą spełniającą nierówność 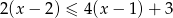 jest
jest
A) 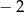 B)
B) 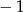 C) 0 D) 1
C) 0 D) 1
Na rysunku przedstawiono fragment prostej o równaniu 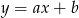 .
.
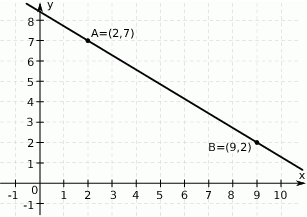
Punkt 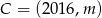 leży na tej prostej. Zatem
leży na tej prostej. Zatem
A) 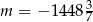 B)
B) 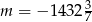 C)
C) 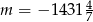 D)
D) 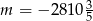
Która z liczb nie może być równa polu rombu o obwodzie 8?
A) 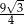 B)
B) 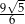 C)
C) 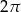 D)
D) 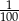
Funkcja 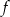 określona jest wzorem
określona jest wzorem 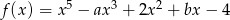 . Jeżeli
. Jeżeli 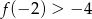 , to
, to
A) 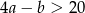 B)
B) 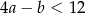 C)
C) 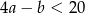 D)
D) 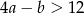
Na rysunku przedstawiono wykres funkcji 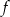 .
.
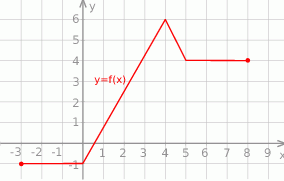
Funkcja 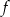 jest malejąca w przedziale
jest malejąca w przedziale
A) 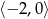 B)
B) 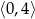 C)
C) 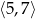 D)
D) 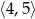
Wykres funkcji liniowej 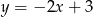 przecina oś
przecina oś 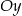 w punkcie o współrzędnych
w punkcie o współrzędnych
A) 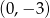 B)
B) 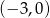 C)
C) 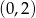 D)
D) 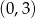
W ciągu geometrycznym 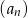 dane są:
dane są: 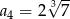 i
i 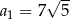 . Wyraz
. Wyraz 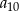 jest równy
jest równy
A) 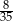 B) 56 C)
B) 56 C) 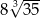 D)
D) 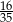
Jeżeli 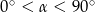 oraz
oraz 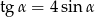 , to
, to
A) 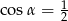 B)
B) 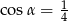 C)
C) 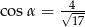 D)
D) 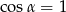
Miary kątów wewnętrznych pewnego pięciokąta pozostają w stosunku 3:4:5:6:9. Najmniejszy kąt wewnętrzny tego pięciokąta ma miarę
A) 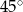 B)
B) 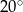 C)
C) 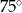 D)
D) 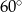
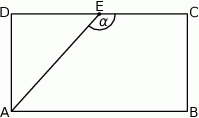
W prostokącie 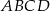 dane są
dane są 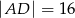 oraz
oraz 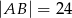 . Punkt
. Punkt 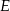 jest środkiem odcinka
jest środkiem odcinka 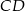 . Wówczas sinus kąta
. Wówczas sinus kąta 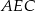 jest równy
jest równy
A)  B)
B)  C)
C) 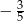 D)
D) 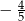
Jeżeli środek okręgu wpisanego w trójkąt leży na wysokości trójkąta, to trójkąt ten musi być
A) rozwartokątny B) prostokątny C) równoramienny D) równoboczny
Przekątne rombu 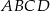 są zawarte w prostych o równaniach:
są zawarte w prostych o równaniach: 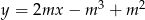 oraz
oraz 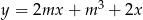 . Zatem
. Zatem
A) 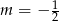 B)
B) 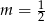 C)
C) 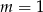 D)
D) 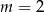
Tworząca stożka o wysokości 3 ma długość 6 (zobacz rysunek).
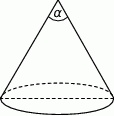
Kąt  rozwarcia tego stożka jest równy
rozwarcia tego stożka jest równy
A) 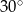 B)
B) 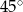 C)
C) 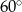 D)
D) 
Objętość walca o promieniu podstawy 3 jest równa 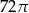 . Pole powierzchni bocznej tego walca jest równe
. Pole powierzchni bocznej tego walca jest równe
A) 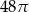 B)
B) 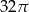 C)
C) 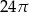 D)
D) 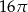
Liczba  jest przybliżeniem z niedomiarem liczby
jest przybliżeniem z niedomiarem liczby  . Błąd względny tego przybliżenia jest równy 4%. Liczba
. Błąd względny tego przybliżenia jest równy 4%. Liczba  jest równa
jest równa
A) 0,585 B) 0,65 C) 0,6 D) 0,665
Każda krawędź graniastosłupa prawidłowego trójkątnego ma długość równą 6. Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 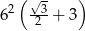 B)
B) 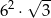 C)
C) 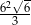 D)
D) 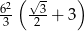
W pewnej grupie przyjaciół co czwarta osoba ma na imię Kuba. Losujemy jedną osobę z tej grupy. Prawdopodobieństwo tego, że wylosowana osoba nie ma na imię Kuba, jest równe
A) 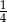 B)
B) 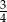 C)
C) 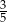 D)
D) 
Zadania otwarte
Rozwiąż nierówność 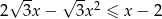 .
.
Mamy dwa pudełka: w pierwszym znajduje się 6 kul ponumerowanych kolejnymi liczbami od 1 do 6, a w drugim – 7 kul ponumerowanych kolejnymi liczbami od 2 do 8. Losujemy po jednej kuli z każdego pudełka i tworzymy liczbę dwucyfrową w ten sposób, że numer kuli wylosowanej z pierwszego pudełka jest cyfrą dziesiątek, a numer kuli wylosowanej z drugiego – cyfrą jedności tej liczby. Oblicz prawdopodobieństwo, że utworzona liczba jest podzielna przez 9.
Przekątne rombu 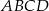 przecinają się w punkcie
przecinają się w punkcie 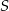 . Punkty
. Punkty 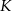 i
i 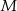 leżą na przekątnej
leżą na przekątnej 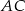 tak, że
tak, że 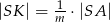 i
i 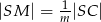 . Punkty
. Punkty 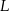 i
i 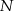 leżą na przekątnej
leżą na przekątnej 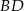 tak, że
tak, że 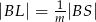 i
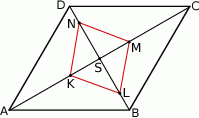
i 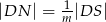 (zobacz rysunek). Wykaż, że jeżeli stosunek pola czworokąta
(zobacz rysunek). Wykaż, że jeżeli stosunek pola czworokąta 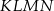 do pola rombu
do pola rombu 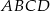 jest równy 1:4, to
jest równy 1:4, to  .
.
Wykaż, że dla dowolnej liczby 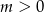 prawdziwa jest nierówność
prawdziwa jest nierówność 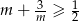 .
.
Jeżeli do licznika i do mianownika nieskracalnego dodatniego ułamka dodamy jego licznik, to otrzymamy  , a jeżeli do licznika i do mianownika dodamy 1, to otrzymamy
, a jeżeli do licznika i do mianownika dodamy 1, to otrzymamy 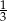 . Wyznacz ten ułamek.
. Wyznacz ten ułamek.
Wyznacz równanie osi symetrii trójkąta o wierzchołkach 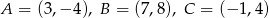 .
.
Dany jest nieskończony rosnący ciąg arytmetyczny 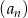 , dla
, dla 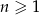 taki, że
taki, że 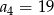 . Wyrazy
. Wyrazy 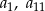 oraz
oraz 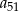 tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem pewnego ciągu geometrycznego. Wyznacz wzór na
tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem pewnego ciągu geometrycznego. Wyznacz wzór na  –ty wyraz ciągu
–ty wyraz ciągu 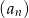 .
.
Funkcja kwadratowa 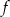 określona jest wzorem
określona jest wzorem 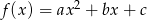 . Zbiorem rozwiązań nierówności
. Zbiorem rozwiązań nierówności 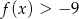 jest przedział
jest przedział 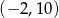 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 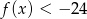 jest zbiór
jest zbiór 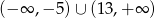 . Oblicz współczynniki
. Oblicz współczynniki 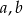 i
i  funkcji
funkcji 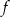 .
.
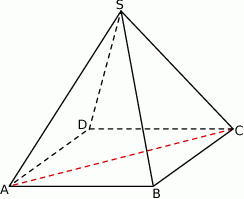
W ostrosłupie prawidłowym czworokątnym 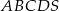 (zobacz rysunek) przekątna
(zobacz rysunek) przekątna 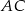 podstawy ma długość 6. Kąt
podstawy ma długość 6. Kąt 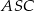 między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę
między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę 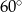 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.