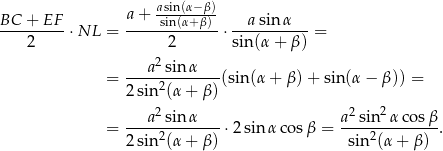Zadanie nr 3145173
W ostrosłupie prawidłowym czworokątnym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 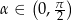 , a krawędź podstawy ma długość
, a krawędź podstawy ma długość  . Przez krawędź podstawy poprowadzono płaszczyznę tworzącą z płaszczyzna podstawy kąt
. Przez krawędź podstawy poprowadzono płaszczyznę tworzącą z płaszczyzna podstawy kąt 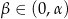 . Wykaż, że pole otrzymanego przekroju jest równe
. Wykaż, że pole otrzymanego przekroju jest równe
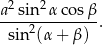
Rozwiązanie
Szkicujemy opisaną sytuację.
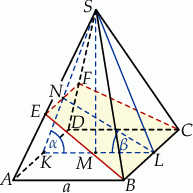
Przekrój 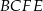 , o którym mowa w treści zadania to trapez równoramienny o jednej podstawie
, o którym mowa w treści zadania to trapez równoramienny o jednej podstawie 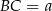 . Łatwo też obliczyć wysokość
. Łatwo też obliczyć wysokość 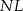 tego trapezu – stosujemy twierdzenie sinusów w trójkącie
tego trapezu – stosujemy twierdzenie sinusów w trójkącie 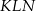 .
.
Ostatni element jaki jest nam potrzebny do obliczenia pola trapezu 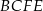 to długość podstawy
to długość podstawy 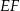 . Obliczymy ją oczywiście w trójkącie
. Obliczymy ją oczywiście w trójkącie 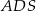 , ale zanim to zrobimy, spróbujemy obliczyć skalę
, ale zanim to zrobimy, spróbujemy obliczyć skalę 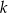 podobieństwa trójkątów
podobieństwa trójkątów 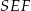 i
i 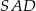 . Zauważmy, że
. Zauważmy, że
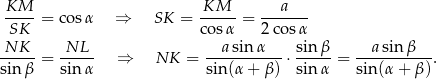
W takim razie interesująca nas skala podobieństwa 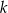 jest równa
jest równa
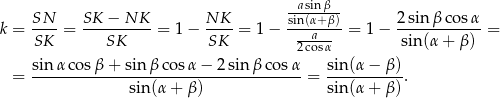
Ten sam wynik mogliśmy otrzymać odrobinę szybciej pisząc twierdzenie sinusów w trójkącie 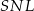 , w którym
, w którym 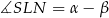 ,
, 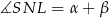 i
i 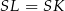 .
.
Teraz łatwo już obliczyć długość odcinka 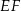 .
.
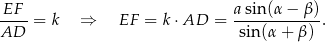
Pole trapezu  jest równe
jest równe