Zadanie nr 3495910
Długość krawędzi podstawy ostrosłupa prawidłowego czworokątnego 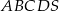 jest równa
jest równa  , a wysokość tego ostrosłupa ma długość
, a wysokość tego ostrosłupa ma długość 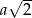 . Punkty
. Punkty 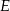 i
i 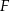 są środkami krawędzi bocznych odpowiednio
są środkami krawędzi bocznych odpowiednio 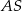 i
i 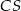 . Oblicz obwód trójkąta
. Oblicz obwód trójkąta 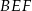 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
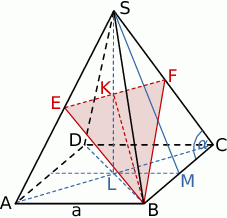
Odcinek 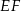 jest odcinkiem łączącym środki boków w trójkącie
jest odcinkiem łączącym środki boków w trójkącie 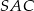 , więc
, więc
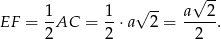
Sposób I
Dorysujmy wysokość 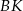 trójkąta równoramiennego
trójkąta równoramiennego 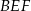 . W trójkącie prostokątnym
. W trójkącie prostokątnym 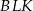 mamy
mamy
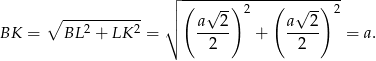
Teraz patrzymy na trójkąt prostokątny 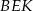 .
.
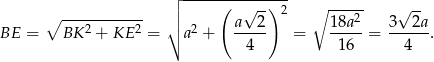
Interesujący nas obwód trójkąta 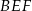 jest więc równy
jest więc równy
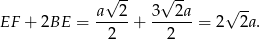
Sposób II
Tym razem skorzystamy z twierdzenia cosinusów w trójkącie 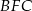 . Zauważmy najpierw, że
. Zauważmy najpierw, że
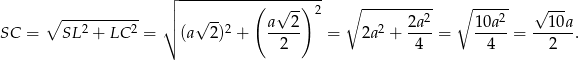
Jeżeli oznaczymy 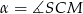 , to
, to
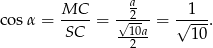
Piszemy teraz twierdzenie cosinusów w trójkącie 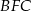 .
.
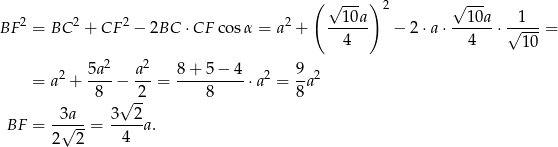
Interesujący nas obwód trójkąta 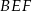 jest więc równy
jest więc równy
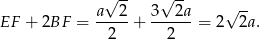
Odpowiedź: