Zadanie nr 4763804
W ostrosłupie prawidłowym czworokątnym pole podstawy jest równe 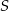 , a kąt nachylenia ściany bocznej do płaszczyzny podstawy ma miarę
, a kąt nachylenia ściany bocznej do płaszczyzny podstawy ma miarę  . Ostrosłup przecięto płaszczyzną zawierającą krawędź boczną tego ostrosłupa i przechodzącą przez środek rozłącznej z nią krawędzi podstawy. Oblicz pole otrzymanego przekroju.
. Ostrosłup przecięto płaszczyzną zawierającą krawędź boczną tego ostrosłupa i przechodzącą przez środek rozłącznej z nią krawędzi podstawy. Oblicz pole otrzymanego przekroju.
Rozwiązanie
Zcznijmy od rysunku i chwilę się zastanówmy.
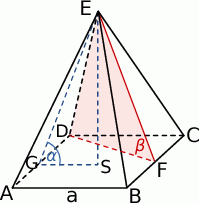
Podane pole podstawy 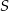 daje nam krawędź
daje nam krawędź  podstawy
podstawy
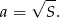
Z podanego kąta  łatwo wyliczymy wysokość i krawędź ściany bocznej. Innymi słowy widać, że jesteśmy w stanie wyliczyć wszystkie boki trójkąta
łatwo wyliczymy wysokość i krawędź ściany bocznej. Innymi słowy widać, że jesteśmy w stanie wyliczyć wszystkie boki trójkąta 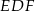 . To powinno (przynajmniej teoretycznie – wzór Herona, brrr) pozwolić nam wyliczyć pole tego trójkąta.
. To powinno (przynajmniej teoretycznie – wzór Herona, brrr) pozwolić nam wyliczyć pole tego trójkąta.
Liczymy
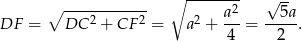
Dalej,
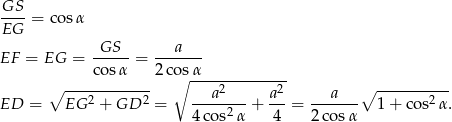
W tym miejscu prawdziwi twardziele podstawiają do wzoru Herona i liczą. Nam jednak do takiej drogi brakuje odwagi, więc spróbujmy to zrobić inaczej. Z twierdzenia cosinusów policzymy cosinus jednego z kątów trójkąta 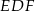 , potem z cosinusa sinus i będziemy mieli pole. Liczymy
, potem z cosinusa sinus i będziemy mieli pole. Liczymy
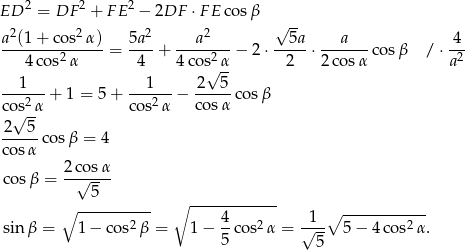
No i możemy policzyć szukane pole
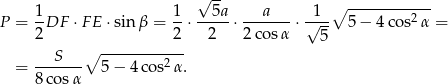
Odpowiedź: