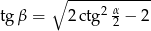/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny/Przekroje

Zadanie nr 6585472

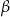W ostrosłupie prawidłowym czworokątnym kąt ostry ściany bocznej przy wierzchołku ostrosłupa ma miarę α . Oblicz tangens kąta ostrego β , jaki tworzy z płaszczyzną podstawy płaszczyzna przechodząca przez wierzchołek ostrosłupa oraz przez środki dwóch sąsiednich boków podstawy.

Wersja PDF

Rozwiązanie

Zaczynamy od rysunku.

PIC

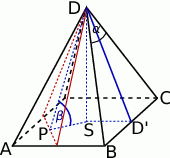
W podstawie ostrosłupa jest kwadrat, oznaczmy jego bok przez 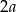2a (oznaczamy przez 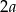2a , żeby było mniej ułamków).

Aby wyliczyć szukany tangens, potrzebujemy znać długości odcinków 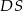DS (czyli wysokość ostrosłupa) oraz 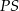P S . Ten drugi to po prostu czwarta część przekątnej kwadratu w podstawie, czyli

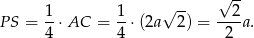
√ -- √ -- PS = 1-⋅AC = 1⋅ (2a 2) = --2-a. 4 4 2

Pozostało wyliczyć 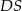DS . Wyliczymy to oczywiście z trójkąta prostokątnego 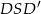DSD ′ , ale najpierw musimy wyliczyć 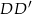DD ′ . Z trójkąta prostokątnego 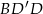BD ′D , mamy

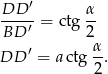
DD--′ α- BD ′ = ctg 2 ′ α DD = a ctg 2-.

Korzystamy teraz z twierdzenia Pitagorasa w trójkącie 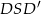DSD ′

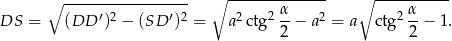
∘ -------------- ∘ ----------- ∘ ----------------- 2 α 2 α DS = (DD ′)2 − (SD ′)2 = a2 ctg --− a2 = a ctg --− 1. 2 2

Mamy zatem

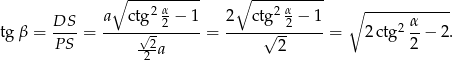
∘ ----2 α--- ∘ ---2-α---- ∘ ------------ DS a c tg 2 − 1 2 ctg 2 − 1 2 α tgβ = P-S-= -----√2-------= -----√--------= 2ctg 2-− 2. -2 a 2

 
Odpowiedź: ∘ ----2-α----- tg β = 2ctg 2 − 2

Wersja PDF