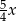Zadanie nr 8744559
Pole przekroju ostrosłupa prawidłowego czworokątnego płaszczyzną przechodzącą przez przekątną podstawy i równoległą do krawędzi bocznej rozłącznej z tą przekątną wynosi  . Oblicz pole przekroju ostrosłupa płaszczyzną zawierającą środki dwóch sąsiednich boków podstawy i środek wysokości ostrosłupa.
. Oblicz pole przekroju ostrosłupa płaszczyzną zawierającą środki dwóch sąsiednich boków podstawy i środek wysokości ostrosłupa.
Rozwiązanie
Jest to jedno z tych zadań, że dobry rysunek w zasadzie załatwia sprawę.
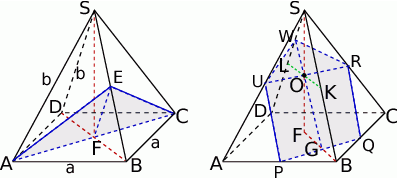
Jeżeli oznaczymy krawędź podstawy przez  , a krawędź boczną przez
, a krawędź boczną przez 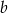 to pierwsza informacja mówi nam, że
to pierwsza informacja mówi nam, że
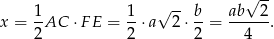
Powyżej skorzystaliśmy z tego, że 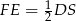 – a tak jest na mocy twierdzenia Talesa w trójkącie
– a tak jest na mocy twierdzenia Talesa w trójkącie 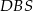 .
.
Czas zająć się drugim przekrojem. Na początku może być ciężko, ale jak trochę sobie porysujemy, to widać, że wyjdzie pewien pięciokąt 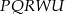 . Spróbujmy ustalić gdzie dokładnie są jego wierzchołki. Ponieważ odcinek
. Spróbujmy ustalić gdzie dokładnie są jego wierzchołki. Ponieważ odcinek 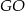 łączy środki boków w trójkącie
łączy środki boków w trójkącie 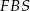 , więc jest równoległy do krawędzi
, więc jest równoległy do krawędzi 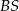 . Zatem cały przekrój jest równoległy do tej krawędzi, w szczególności odcinki
. Zatem cały przekrój jest równoległy do tej krawędzi, w szczególności odcinki 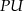 i
i 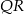 muszą być do niej równoległe, czyli czworokąt
muszą być do niej równoległe, czyli czworokąt 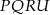 jest prostokątem. Ponieważ
jest prostokątem. Ponieważ 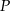 i
i 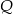 są środkami krawędzi
są środkami krawędzi 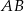 i
i 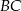 to
to
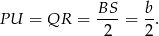
Policzmy od razu pole prostokąta 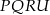 :
:
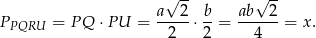
Pozostało się zająć trójkątem 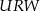 . Jego podstawa ma długość
. Jego podstawa ma długość
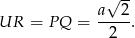
Aby wyznaczyć jego wysokość 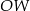 , połączmy ze sobą środki
, połączmy ze sobą środki 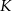 i
i 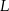 krawędzi
krawędzi 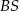 i
i 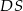 . W powstałym trójkącie
. W powstałym trójkącie 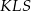 odcinek
odcinek 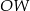 przechodzi przez środek boku
przechodzi przez środek boku 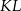 i jest równoległy do
i jest równoległy do 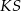 (bo już wcześniej ustaliliśmy, że
(bo już wcześniej ustaliliśmy, że 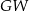 i
i 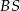 są równoległe). Zatem
są równoległe). Zatem
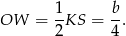
Zatem pole trójkąta  jest równe
jest równe
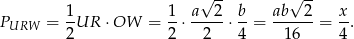
Pole całego przekroju jest równe
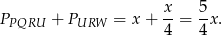
Odpowiedź: