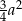/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny/Przekroje

Zadanie nr 9420477

Dodaj do ulubionych
Dodaj do rozwiązanych

Wysokość ostrosłupa prawidłowego czworokątnego jest 2 razy dłuższa od krawędzi jego podstawy. Przez przekątną podstawy i środek rozłącznej z nią krawędzi bocznej poprowadzono płaszczyznę. Oblicz pole otrzymanego przekroju, wiedząc, że krawędź podstawy ostrosłupa ma długość a .

Rozwiązanie

Zacznijmy od rysunku.

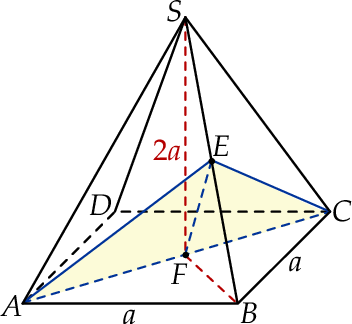
ZINFO-FIGURE

Po pierwsze znamy podstawę trójkąta będącego opisanym przekrojem.

√ -- AC = a 2.

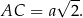
Pozostało obliczyć jego wysokość 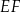EF .

Sposób I

Obliczymy ją z trójkąta prostokątnego FBS . W tym trójkącie mamy

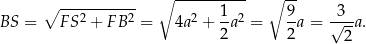
∘ ---------- ∘ -- ∘ ---2-----2- 2 1- 2 9- -3-- BS = FS + FB = 4a + 2a = 2 a = √ 2-a.

Ponadto

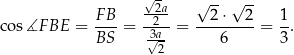
√- √ --√ -- FB -22a- 2⋅ 2 1 cos∡F BE = BS- = -3√a- = ---6---- = 3-. 2

Stosujemy teraz twierdzenie cosinusów do trójkąta 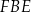F BE .

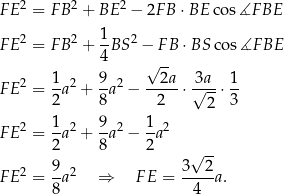
F E2 = F B2 + BE 2 − 2FB ⋅BE cos∡F BE 1 F E2 = F B2 + --BS2 − F B ⋅BS cos ∡F BE 4 √ -- 2 1 2 9 2 2a 3a 1 F E = 2a + 8a − --2--⋅ √---⋅3- 2 F E2 = 1a2 + 9a2 − 1-a2 2 8 2 9 3 √ 2- F E2 = -a2 ⇒ F E = -----a. 8 4

Pozostało policzyć pole

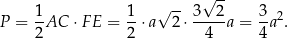
√ -- 1- 1- √ -- 3--2- 3-2 P = 2AC ⋅F E = 2 ⋅ a 2⋅ 4 a = 4a .

Sposób II

Tak naprawdę, odcinek 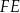FE mogliśmy obliczyć znacznie prościej zauważając, że jest to środkowa w trójkącie prostokątnym 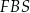FBS , a długość środkowej opuszczonej na przeciwprostokątną w trójkącie prostokątnym jest równa połowie przeciwprostokątnej (bo obie te długości to promień okręgu opisanego na trójkącie). Zatem 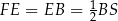FE = EB = 12BS . Długość odcinka 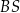BS i pole liczymy jak poprzednio.  
Odpowiedź: 3a 2 4

Wersja PDF