Zadanie nr 9476529
Uzasadnij, że istnieje jedna para 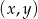 liczb całkowitych
liczb całkowitych 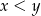 , których suma jest równa 23, a ich iloczyn jest równy 132.
, których suma jest równa 23, a ich iloczyn jest równy 132.
Rozwiązanie
Jeżeli  i
i 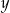 są takimi liczbami to spełniają układ równań
są takimi liczbami to spełniają układ równań
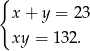
Podstawiamy 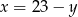 z pierwszego równania do drugiego.
z pierwszego równania do drugiego.
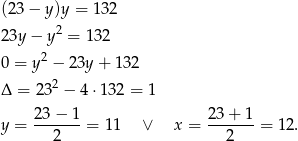
Wtedy odpowiednio 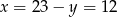 i
i 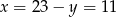 . Z założenia
. Z założenia 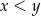 wynika, że
wynika, że 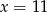 i
i 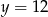 .
.

