/Szkoła średnia/Zadania maturalne/Matura 2016/Matura

Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom rozszerzony
(stara formuła) 3 czerwca 2016 Czas pracy: 180 minut

Zadanie 1
(4 pkt)

Rozwiąż nierówność 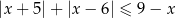|x + 5|+ |x − 6 | ≤ 9 − x .

Zadanie 2
(4 pkt)

Rozwiąż równanie 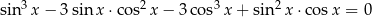sin 3x − 3 sin x ⋅cos2x − 3 cos3x + sin2 x ⋅cosx = 0 w przedziale ⟨0,π ⟩ .

Zadanie 3
(5 pkt)

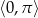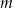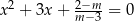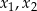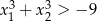Wyznacz wszystkie wartości parametru m , dla których równanie x2 + 3x + 2−m--= 0 m−3 ma dwa różne rozwiązania rzeczywiste x1,x2 spełniające warunek 3 3 x1 + x2 > − 9 .

Zadanie 4
(3 pkt)

Ciąg 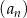(a ) n jest określony wzorem

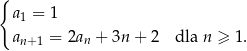
{ a1 = 1 an+1 = 2an + 3n + 2 dla n ≥ 1.

Oblicz średnią arytmetyczną liczb 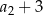a + 3 2 i a + 2 3 .

Zadanie 5
(3 pkt)

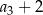Wykaż, że jeśli 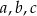a,b,c są dowolnymi liczbami rzeczywistymi takimi, że a + b + c = 0 , to

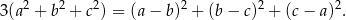
2 2 2 2 2 2 3(a + b + c ) = (a − b) + (b− c) + (c − a) .

Zadanie 6
(4 pkt)

Wyznacz równania stycznych do okręgu 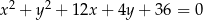x2 + y2 + 12x + 4y + 36 = 0 , przechodzących przez początek układu współrzędnych.

Zadanie 7
(4 pkt)

Rzucamy czterokrotnie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że otrzymamy dokładnie dwie dwójki lub dokładnie dwie piątki. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.

Zadanie 8
(5 pkt)

Dany jest odcinek 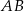AB o długości 10. Rozpatrujemy wszystkie sześciokąty foremne 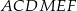ACDMEF i trójkąty równoboczne 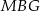MBG , których wspólny wierzchołek 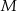M leży na odcinku 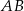AB (zobacz rysunek).

PIC

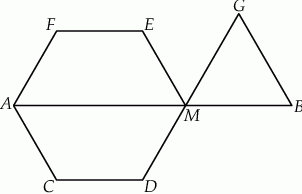
Oblicz stosunek obwodu sześciokąta 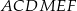ACDMEF do obwodu trójkąta 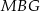MBG w przypadku, gdy suma pól tych dwóch wielokątów jest najmniejsza.

Zadanie 9
(4 pkt)

Dany jest czworokąt wypukły 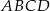ABCD , w którym: 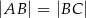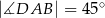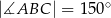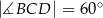|AB | = |BC | , |∡DAB | = 45∘ , |∡ABC | = 150∘ , |∡BCD | = 60∘ . Wykaż, że trójkąt 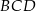BCD jest równoboczny.

Zadanie 10
(4 pkt)

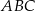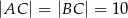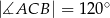Dany jest trójkąt ABC , w którym |AC | = |BC | = 10 , |∡ACB | = 120∘ . Na boku 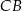CB obrano punkt 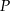P dzielący ten bok w stosunku 3:2 (licząc od punktu 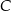C ). Oblicz sinus kąta PAB .

Zadanie 11
(4 pkt)

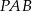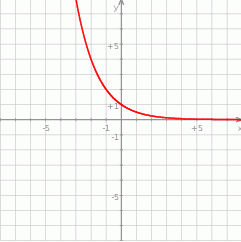
Na rysunku przedstawiono fragment wykresu funkcji wykładniczej określonej wzorem 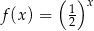( )x f(x) = 12 . Rozważamy funkcję 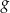g określoną wzorem 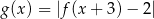g(x) = |f(x + 3 )− 2 | . Wyznacz wszystkie wartości parametru 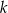k , dla których równanie 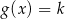g(x ) = k ma dwa rozwiązania takie, że ich iloczyn jest liczbą ujemną.

PIC

Zadanie 12
(6 pkt)

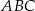Trójkąt ABC jest podstawą prawidłowego ostrosłupa 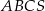ABCS , którego krawędź boczna ma długość 10. Punkt 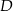D jest środkiem wysokości 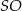SO ostrosłupa oraz 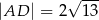√ --- |AD | = 2 13 . Oblicz objętość tego ostrosłupa.

Arkusz Wersja PDF
Rozwiązania