/Szkoła średnia/Zadania maturalne/Matura 2017
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 8 kwietnia 2017 Czas pracy: 170 minut
Zadania zamknięte
Dla każdej dodatniej liczby  wyrażenie
wyrażenie 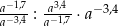 jest równe
jest równe
A) 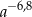 B)
B) 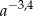 C) 1 D)
C) 1 D) 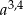
Kurtkę, która kosztowała 450 złotych, przeceniono i sprzedano za 387 złotych. O ile procent obniżono cenę kurtki?
A) 14 B) 15 C) 20 D) 24
Liczba o 2 większa od liczby 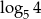 jest równa
jest równa
A) 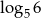 B)
B) 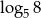 C)
C) 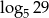 D)
D) 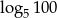
Liczba 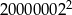 jest równa
jest równa
A) 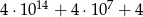 B)
B) 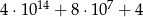 C) 40 000 004 D)
C) 40 000 004 D) 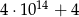
Jedną z liczb, które spełniają nierówność 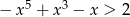 , jest
, jest
A) 1 B) 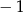 C) 2 D)
C) 2 D) 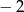
Funkcja kwadratowa określona jest wzorem 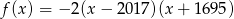 . Wynika stąd, że
. Wynika stąd, że
A) 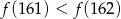 B)
B) 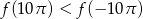 C)
C) 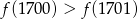 D)
D) 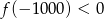
Funkcja 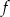 określona jest wzorem
określona jest wzorem 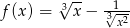 . Wtedy liczba
. Wtedy liczba 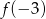 jest równa
jest równa
A) 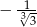 B)
B) 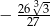 C)
C) 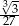 D)
D) 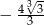
Na rysunku 1. jest przedstawiony wykres funkcji  , a na rysunku 2. – wykres funkcji
, a na rysunku 2. – wykres funkcji  .
.
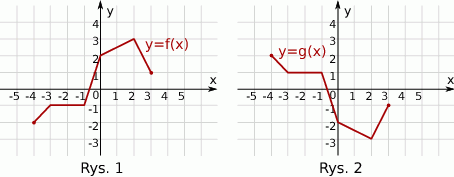
Funkcja  jest określona wzorem
jest określona wzorem
A) 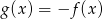 B)
B) 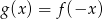 C)
C) 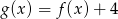 D)
D) 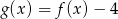
Równanie wymierne 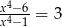 , gdzie
, gdzie 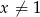 i
i 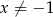 ,
,
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dokładnie dwa rozwiązania rzeczywiste.
D) ma dokładnie cztery rozwiązania rzeczywiste.
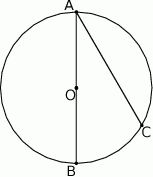
Odcinek 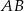 jest średnicą okręgu o środku w punkcie
jest średnicą okręgu o środku w punkcie 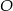 i promieniu
i promieniu  (zobacz rysunek). Cięciwa
(zobacz rysunek). Cięciwa 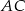 ma długość
ma długość 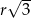 , więc
, więc
A) 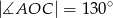 B)
B) 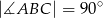 C)
C) 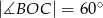 D)
D) 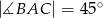
Dla każdej liczby całkowitej dodatniej  suma
suma  początkowych wyrazów ciągu geometrycznego
początkowych wyrazów ciągu geometrycznego 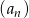 jest określona wzorem
jest określona wzorem 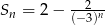 . Wtedy iloraz
. Wtedy iloraz 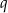 tego ciągu jest równy
tego ciągu jest równy
A) 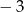 B)
B) 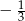 C)
C) 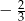 D)
D) 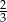
Jeżeli  i
i 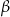 są miarami kątów ostrych trójkąta prostokątnego oraz
są miarami kątów ostrych trójkąta prostokątnego oraz 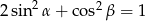 to
to
A) 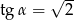 B)
B) 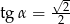 C)
C) 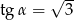 D)
D) 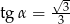
Na której z podanych prostych leżą wszystkie punkty o współrzędnych 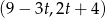 , gdzie
, gdzie 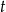 jest dowolną liczbą rzeczywistą?
jest dowolną liczbą rzeczywistą?
A) 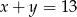 B)
B) 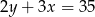 C)
C) 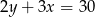 D)
D) 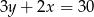
Ile jest wszystkich czterocyfrowych liczb naturalnych podzielnych przez 3?
A) 3000 B) 3333 C) 2999 D) 2998
Punkty 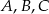 i
i 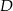 leżą na okręgu o środku
leżą na okręgu o środku 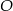 (zobacz rysunek). Miary zaznaczonych kątów
(zobacz rysunek). Miary zaznaczonych kątów  i
i 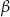 są odpowiednio równe
są odpowiednio równe
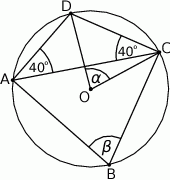
A) 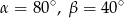 B)
B) 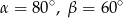 C)
C) 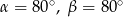 D)
D) 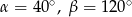
Promień kuli o polu powierzchni równym 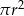 powiększono 2 razy. Objętość tak zmienionej kuli jest równa
powiększono 2 razy. Objętość tak zmienionej kuli jest równa
A) 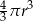 B)
B) 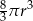 C)
C) 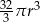 D)
D) 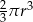
Prosta określona wzorem 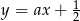 jest symetralną odcinka
jest symetralną odcinka 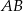 , gdzie
, gdzie 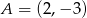 i
i 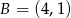 . Wynika stąd, że
. Wynika stąd, że
A) 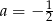 B)
B) 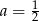 C)
C) 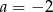 D)
D) 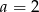
Z odcinków o długościach: 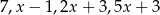 można zbudować trapez równoramienny. Wynika stąd, że
można zbudować trapez równoramienny. Wynika stąd, że
A) 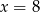 B)
B) 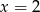 C)
C) 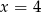 D)
D) 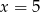
Na rysunku przedstawiono wykresy trzech parami przecinających się prostych
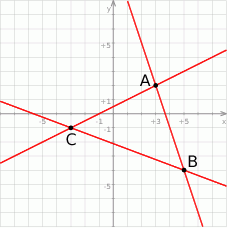
Te proste to
A) 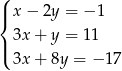 B)
B) 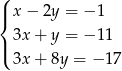 C)
C) 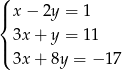 D)
D) 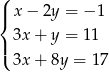
Podstawą ostrosłupa prawidłowego czworokątnego  jest kwadrat
jest kwadrat 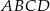 . Jaka jest miara kąta
. Jaka jest miara kąta 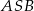 jeżeli trójkąt
jeżeli trójkąt 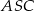 jest prostokątny?
jest prostokątny?
A) 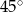 B)
B) 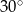 C)
C) 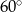 D)
D) 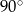
Trójwyrazowy ciąg 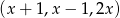 jest arytmetyczny dla
jest arytmetyczny dla
A) 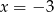 B)
B) 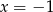 C)
C) 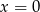 D)
D) 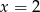
Rzucamy trzy razy symetryczną monetą. Niech 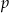 oznacza prawdopodobieństwo otrzymania co najwyżej jednej reszki w tych trzech rzutach. Wtedy
oznacza prawdopodobieństwo otrzymania co najwyżej jednej reszki w tych trzech rzutach. Wtedy
A) 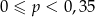 B)
B) 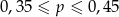 C)
C) 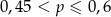 D)
D) 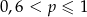
Trójkąt 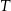 jest podobny do trójkąta
jest podobny do trójkąta 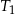 w skali
w skali 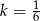 , a trójkąt
, a trójkąt 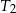 jest podobny do trójkąta
jest podobny do trójkąta 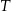 w skali
w skali 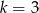 . Pole trójkąta
. Pole trójkąta 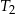 jest równe 24. Trójkąt
jest równe 24. Trójkąt 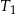 ma pole równe
ma pole równe
A) 12 B) 48 C) 72 D) 96
Dane są dwie sumy algebraiczne 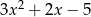 oraz
oraz 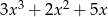 . Iloczyn tych sum jest równy
. Iloczyn tych sum jest równy
A) 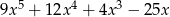
B) 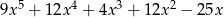
C) 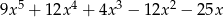
D) 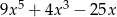
Rzucono 100 razy sześcienną kostką do gry. Średnia arytmetyczna liczb oczek w pierwszych 40 rzutach była równa 3,75, a średnia arytmetyczna liczb oczek w kolejnych 60 rzutach była równa 4,25. Średnia arytmetyczna liczb oczek w 100 rzutach jest
A) mniejsza od 4 B) równa 4 C) równa 4,05 D) większa od 4,05
Zadania otwarte
Rozwiąż równanie 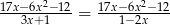 , gdzie
, gdzie 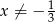 i
i 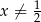 .
.
Funkcja kwadratowa jest określona wzorem 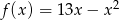 . Oblicz największą wartość funkcji
. Oblicz największą wartość funkcji 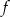 w przedziale
w przedziale 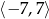 .
.
W tabeli przedstawiono informację o długości stóp uczniów klasy IIIc.
| liczba uczniów | 1 | 3 | 2 | 4 | 3 | 5 | 3 | 4 |
| długość stopy (w cm) | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
Oblicz średnią długość stopy ucznia tej klasy. Otrzymany wynik zaokrąglij do 1 cm. Oblicz błąd względny otrzymanego przybliżenia.
Prosta przechodząca przez wierzchołek 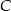 kwadratu
kwadratu 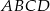 przecina przedłużenia jego boków
przecina przedłużenia jego boków 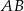 i
i 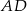 odpowiednio w punktach
odpowiednio w punktach 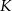 i
i 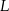 (zobacz rysunek).
(zobacz rysunek).
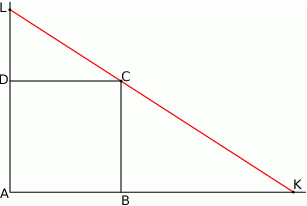
Wykaż, że
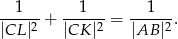
Ciąg 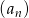 jest określony wzorem
jest określony wzorem 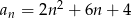 dla
dla 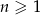 . Wykaż, że suma każdych dwóch kolejnych wyrazów tego ciągu jest kwadratem liczby naturalnej.
. Wykaż, że suma każdych dwóch kolejnych wyrazów tego ciągu jest kwadratem liczby naturalnej.
Rozwiąż nierówność: 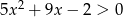 .
.
Dane są dwa wierzchołki 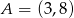 i
i 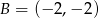 prostokąta
prostokąta 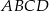 oraz punkt
oraz punkt 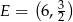 leżący na prostej
leżący na prostej 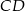 . Wyznacz współrzędne wierzchołków
. Wyznacz współrzędne wierzchołków 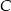 i
i 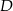 tego prostokąta.
tego prostokąta.
Wysokość ostrosłupa prawidłowego trójkątnego jest dwa razy krótsza od promienia okręgu opisanego na podstawie tego ostrosłupa, a jego objętość jest równa 9. Oblicz pole powierzchni bocznej ostrosłupa oraz tangens kąta, jaki tworzy krawędź boczna z krawędzią podstawy ostrosłupa.
Rejsowy samolot z Warszawy do Paryża przelatuje nad Niemcami każdorazowo tą samą trasą z taką samą zakładaną prędkością przelotową. W poniedziałek jego średnia prędkość była o 20% mniejsza niż prędkość przelotowa, a w środę średnia prędkość była o 20% większa od zakładanej prędkości przelotowej. Czas przelotu nad Niemcami w poniedziałek różnił się od czasu przelotu w środę o 28 minut. Jak długo trwał przelot tego samolotu nad Niemcami w poniedziałek?

