/Szkoła średnia/Zadania maturalne/Matura 2017/Matura próbna
Lubelska próba przed maturą
z matematyki poziom podstawowy grupa I
28 lutego 2017 Czas pracy: 170 minut
Zadania zamknięte
Rozwiązaniem nierówności 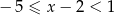 jest zbiór
jest zbiór
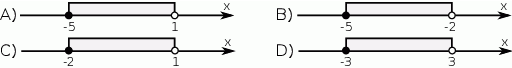
Wartość wyrażenia 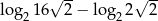 jest równa
jest równa
A) 3 B) 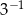 C)
C) 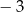 D)
D) 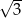
Karolina ma o 25% wyższy wynik z egzaminu próbnego od Oli. Wynika z tego, że Oli wynik jest niższy od wyniku Karoliny o
A) 25% B) 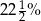 C) 20% D)
C) 20% D) 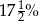
Jeżeli 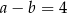 i
i 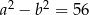 , to
, to 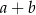 jest równe
jest równe
A) 14 B) 16 C) 18 D) 20
Rozwiązaniem układu równań 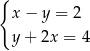 w prostokątnym układzie współrzędnych na płaszczyźnie jest
w prostokątnym układzie współrzędnych na płaszczyźnie jest
A) prosta 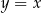 B) dwa punkty C) zbiór pusty D) jeden punkt
B) dwa punkty C) zbiór pusty D) jeden punkt
Iloczyn wszystkich pierwiastków równania 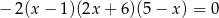 jest równy
jest równy
A) 15 B) 30 C) 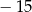 D)
D) 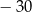
Rozwiązaniem równania 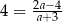 jest liczba
jest liczba
A) 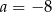 B)
B) 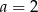 C)
C) 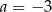 D)
D) 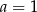
Dziedziną funkcji, której wykres przedstawiono na rysunku jest
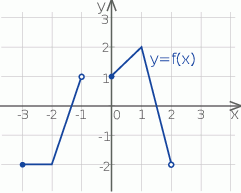
A) 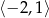 B)
B) 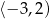 C)
C) 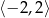 D)
D) 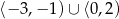
Punkt o współrzędnych 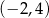 należy do prostej
należy do prostej 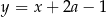 . Zatem
. Zatem
A) 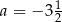 B)
B) 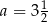 C)
C) 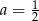 D)
D) 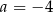
Liczba 4 jest miejscem zerowym funkcji liniowej 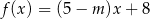 . Wynika stąd, że
. Wynika stąd, że
A) 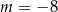 B)
B) 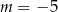 C)
C) 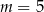 D)
D) 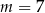
Funkcja kwadratowa 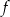 przyjmuje wartość największą równą
przyjmuje wartość największą równą 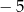 dla argumentu równego 2. Ten warunek spełnia funkcja o równaniu:
dla argumentu równego 2. Ten warunek spełnia funkcja o równaniu:
A) 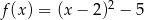 B)
B) 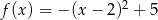
C) 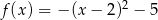 D)
D) 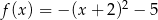
Największą liczbą całkowitą spełniającą nierówność 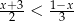 jest
jest
A) 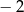 B) 2 C) 1 D)
B) 2 C) 1 D) 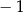
Dany jest ciąg liczbowy 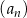 , w którym
, w którym 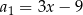 ,
, 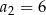 ,
, 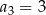 . Dla jakiej wartości liczbowej
. Dla jakiej wartości liczbowej  dany ciąg jest ciągiem geometrycznym?
dany ciąg jest ciągiem geometrycznym?
A) 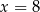 B)
B) 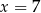 C)
C) 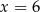 D)
D) 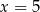
Tangens kąta  zaznaczonego na rysunku jest równy
zaznaczonego na rysunku jest równy
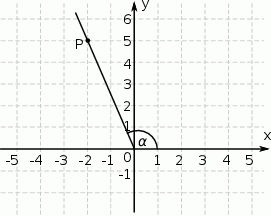
A) 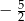 B)
B)  C)
C) 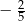 D)
D) 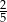
Jeżeli 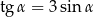 , oraz
, oraz  jest kątem ostrym, to
jest kątem ostrym, to
A) 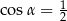 B)
B) 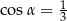 C)
C) 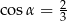 D)
D) 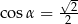
Jeżeli suma miar kąta środkowego i kąta wpisanego opartych na tym samym łuku jest równa 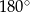 , to kąty te są oparte na
, to kąty te są oparte na
A) 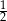 okręgu B)
okręgu B)  okręgu C)
okręgu C) 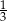 okręgu D)
okręgu D) 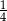 okręgu
okręgu
Przekątna prostokąta ma długość 12 cm i tworzy z jednym z boków kąt o mierze 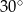 . Pole powierzchni tego prostokąta jest równe
. Pole powierzchni tego prostokąta jest równe
A) 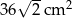 B)
B) 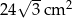 C)
C) 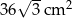 D)
D) 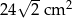
Proste o równaniach 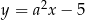 oraz
oraz 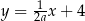 (
(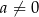 ) są prostopadłe dla
) są prostopadłe dla  równego
równego
A) 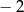 B) 2 C) 1 D)
B) 2 C) 1 D) 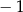
Suma dwóch początkowych wyrazów ciągu arytmetycznego 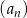 wynosi 5, a trzeci wyraz jest równy 7. Wówczas
wynosi 5, a trzeci wyraz jest równy 7. Wówczas
A) 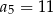 B)
B) 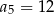 C)
C) 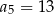 D)
D) 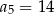
Środkiem odcinka o końcach 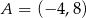 i
i 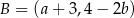 jest początek prostokątnego układu współrzędnych. Wówczas
jest początek prostokątnego układu współrzędnych. Wówczas
A) 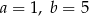 B)
B) 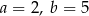 C)
C) 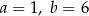 D)
D) 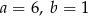
Dany jest graniastosłup prawidłowy czworokątny (patrz rysunek). Podaj oznaczenie kąta zawartego między przekątną graniastosłupa i krawędzią podstawy.
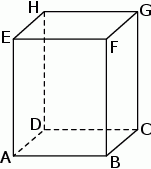
A) 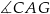 B)
B) 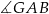 C)
C) 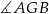 D)
D) 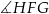
Pole przekroju osiowego walca jest równe 12. Pole powierzchni bocznej tego walca jest równe
A) 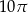 B)
B) 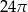 C)
C) 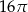 D)
D) 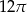
Przekątna graniastosłupa prawidłowego czworokątnego o długości równej 10 cm jest nachylona do płaszczyzny podstawy pod kątem 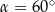 . Wysokość tego graniastosłupa ma długość równą
. Wysokość tego graniastosłupa ma długość równą
A) 5 cm B) 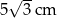 C)
C) 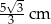 D)
D) 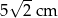
Dla jakiej wartości liczbowej  średnia arytmetyczna liczb:
średnia arytmetyczna liczb: 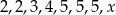 jest równa 4?
jest równa 4?
A) 6 B) 5 C) 4 D) 3
Losujemy rzucając dwukrotnie symetryczną kostką sześcienną. Jakie jest prawdopodobieństwo, że w drugim rzucie wylosujemy o trzy oczka więcej niż w pierwszym?
A) 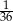 B)
B) 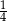 C)
C) 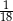 D)
D) 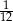
Zadania otwarte
Rozwiąż nierówność: 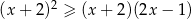 .
.
Wykaż, że dla dowolnych liczb całkowitych 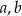 liczba
liczba 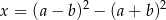 jest podzielna przez 4.
jest podzielna przez 4.
Wykaż, że stosunek długości promienia okręgu opisanego na kwadracie do długości promienia wpisanego w ten kwadrat jest równy 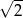 .
.
Oblicz najmniejszą i największą wartość funkcji 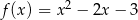 w przedziale
w przedziale 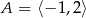 .
.
Dane są punkty 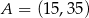 i
i 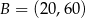 . Wyznacz współrzędne punktu przecięcia prostej
. Wyznacz współrzędne punktu przecięcia prostej 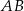 z osią
z osią 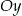 .
.
Średnia arytmetyczna dwóch liczb wynosi 20. Jeśli jedną z nich zwiększymy dwukrotnie, a drugą zmniejszymy o 50%, to średnia arytmetyczna zwiększy się o 2. Wyznacz te liczby.
W graniastosłupie prawidłowym trójkątnym przekątna ściany bocznej tworzy z płaszczyzną podstawy kąt o mierze równej 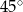 . Oblicz pole powierzchni bocznej tego graniastosłupa, wiedząc, że jego objętość jest równa
. Oblicz pole powierzchni bocznej tego graniastosłupa, wiedząc, że jego objętość jest równa 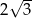 .
.
Ze zbioru 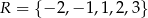 losujemy najpierw jedną liczbę i oznaczamy ją jako
losujemy najpierw jedną liczbę i oznaczamy ją jako  . Następnie z pozostałych liczb losujemy drugą liczbę i oznaczamy ją jako
. Następnie z pozostałych liczb losujemy drugą liczbę i oznaczamy ją jako 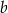 . Liczby
. Liczby  i
i 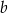 są współczynnikami funkcji kwadratowej
są współczynnikami funkcji kwadratowej 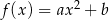 . Oblicz prawdopodobieństwo zdarzenia:
. Oblicz prawdopodobieństwo zdarzenia:
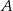 – funkcja
– funkcja 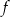 jest malejąca w zbiorze
jest malejąca w zbiorze 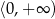 ,
, 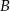 – funkcja
– funkcja 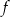 ma dwa różne miejsca zerowe.
ma dwa różne miejsca zerowe.
Ciąg 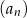 , gdzie
, gdzie 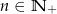 , jest nieskończonym ciągiem arytmetycznym o różnicy 2, w którym pierwszy wyraz jest równy
, jest nieskończonym ciągiem arytmetycznym o różnicy 2, w którym pierwszy wyraz jest równy 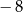 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości 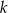 , dla których trzywyrazowy ciąg
, dla których trzywyrazowy ciąg 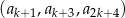 jest ciągiem geometrycznym.
jest ciągiem geometrycznym.

