/Szkoła średnia/Zadania maturalne/Matura 2017/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 22 kwietnia 2017 Czas pracy: 180 minut
Zadania zamknięte
Suma szeregu geometrycznego 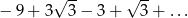 jest równa
jest równa
A) 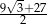 B)
B) 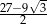 C)
C) 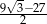 D)
D) 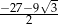
Granica 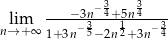 jest równa
jest równa
A) 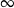 B)
B) 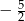 C) 0 D)
C) 0 D) 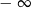
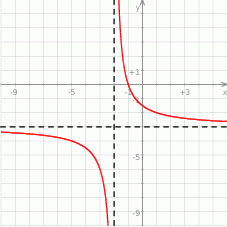
Na rysunku przedstawiono fragment wykresu funkcji homograficznej 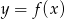 , której dziedziną jest zbiór
, której dziedziną jest zbiór 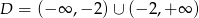 .
.
Równanie 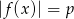 z niewiadomą
z niewiadomą  ma dokładnie jedno rozwiązanie
ma dokładnie jedno rozwiązanie
A) w dwóch przypadkach: 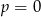 lub
lub 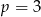 .
.
B) w dwóch przypadkach: 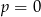 lub
lub 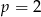 .
.
C) tylko wtedy, gdy 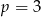 .
.
D) tylko wtedy, gdy 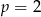 .
.
Równanie 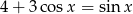 w przedziale
w przedziale 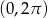
A) ma dokładnie jedno rozwiązanie rzeczywiste.
B) ma dokładnie dwa rozwiązania rzeczywiste.
C) ma więcej niż dwa rozwiązania rzeczywiste.
D) nie ma rozwiązań rzeczywistych.
W równoległoboku 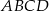 na przekątnej
na przekątnej 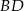 wybrano punkty
wybrano punkty 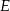 i
i 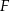 tak, że
tak, że 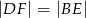 (zobacz rysunek). Dane są ponadto:
(zobacz rysunek). Dane są ponadto: 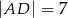 ,
, 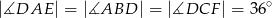 .
.
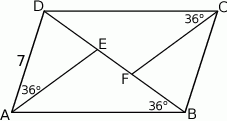
Wówczas długość odcinka 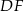 jest równa
jest równa
A) 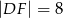 B)
B) 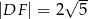 C)
C) 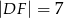 D)
D) 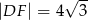
Zadania otwarte
Wśród 1200 uczniów pewnego liceum przeprowadzono sondaż dotyczący funkcjonowania sklepiku szkolnego. Wyniki sondażu przedstawiono w tabeli.
| Badane grupy | Liczba uczniów zadowolonych z asortymentu sklepiku | Liczba uczniów niezadowolonych z asortymentu sklepiku |
| Chłopcy | 320 | 260 |
| Dziewczęta | 280 | 340 |
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrana osoba, spośród ankietowanych, jest zadowolona z asortymentu sklepiku, jeśli wiadomo, że jest dziewczynką.
Oblicz granicę jednostronną funkcji 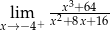 .
.
Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 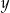 prawdziwa jest nierówność
prawdziwa jest nierówność
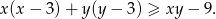
Dany jest sześcian 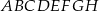 . Przez wierzchołki
. Przez wierzchołki 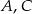 oraz
oraz 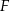 poprowadzono płaszczyznę, która przecina przekątną
poprowadzono płaszczyznę, która przecina przekątną 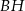 w punkcie
w punkcie 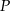 (zobacz rysunek).
(zobacz rysunek).
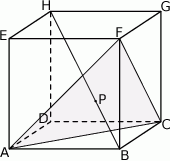
Wykaż, że 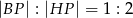 .
.
Wielomian 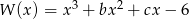 jest podzielny przez trójmian kwadratowy
jest podzielny przez trójmian kwadratowy 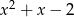 . Wyznacz współczynniki
. Wyznacz współczynniki 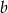 i
i  wielomianu
wielomianu 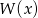 .
.
Na bokach 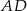 i
i 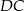 kwadratu
kwadratu 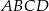 o polu 1 wybrano punkty
o polu 1 wybrano punkty 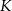 i
i 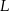 w ten sposób, że
w ten sposób, że 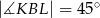 .
.
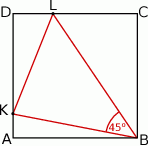
Oblicz odległość punktu 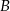 od prostej
od prostej 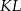 .
.
Oblicz 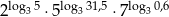 .
.
Rozwiąż nierówność 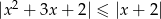 .
.
Ciąg 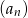 określony dla
określony dla 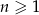 jest rosnący, ma wszystkie wyrazy ujemne oraz spełnia warunki
jest rosnący, ma wszystkie wyrazy ujemne oraz spełnia warunki
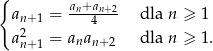
Oblicz iloraz 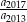 .
.
Punkty 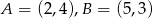 i
i 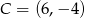 są sąsiednimi wierzchołkami czworokąta
są sąsiednimi wierzchołkami czworokąta 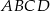 wpisanego w okrąg. Wierzchołek
wpisanego w okrąg. Wierzchołek 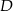 tego czworokąta leży na prostej o równaniu
tego czworokąta leży na prostej o równaniu 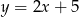 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 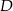 .
.
Wyznacz wszystkie wartości parametru 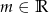 , dla których równanie
, dla których równanie 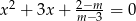 ma dwa różne pierwiastki
ma dwa różne pierwiastki 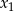 i
i 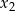 takie, że
takie, że 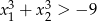 .
.
Z kartonu w kształcie trójkąta równobocznego o boku długości 120 cm odcięto trzy identyczne czworokąty w narożnikach (zobacz rysunek).
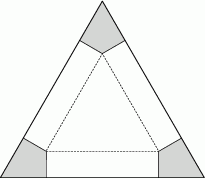
Następnie zagięto karton wzdłuż linii przerywanych, tworząc w ten sposób pudełko w kształcie graniastosłupa trójkątnego prostego (bez przykrywki). Oblicz długość krawędzi podstawy tego pudełka, którego objętość jest największa. Oblicz tę objętość.

