/Szkoła średnia/Zadania maturalne/Matura 2017/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 11 marca 2017 Czas pracy: 180 minut
Zadania zamknięte
Najmniejszą liczbą całkowitą 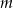 , dla której nierówność:
, dla której nierówność: 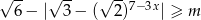 jest sprzeczna jest
jest sprzeczna jest
A) 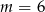 B)
B) 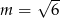 C)
C) 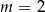 D)
D) 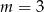
Reszta z dzielenia wielomianu 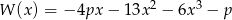 przez dwumian
przez dwumian 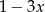 jest równa 3. Zatem
jest równa 3. Zatem
A) 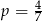 B)
B) 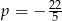 C)
C) 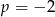 D)
D) 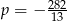
Odległość punktu 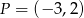 od prostej o równaniu
od prostej o równaniu 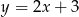 jest równa
jest równa
A) 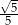 B)
B) 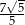 C)
C) 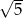 D) 5
D) 5
Cosinus kąta dwuściennego utworzonego przez dwie sąsiednie ściany czworościanu foremnego jest równy
A) 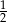 B)
B) 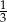 C)
C) 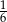 D)
D) 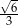
Granica 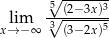 jest równa
jest równa
A) 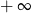 B)
B) 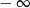 C) 0 D)
C) 0 D) 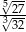
Zadania otwarte
Dany jest ciąg geometryczny 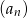 określony wzorem
określony wzorem 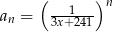 dla
dla 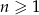 , którego niektóre wyrazy są ujemne. Wyznacz największą liczbę całkowitą
, którego niektóre wyrazy są ujemne. Wyznacz największą liczbę całkowitą  , dla której nieskończony szereg
, dla której nieskończony szereg 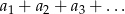 jest zbieżny.
jest zbieżny.
Średnia arytmetyczna  początkowych wyrazów ciągu
początkowych wyrazów ciągu 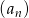 jest równa
jest równa 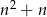 . Wyznacz wzór ogólny ciągu
. Wyznacz wzór ogólny ciągu 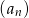 .
.
Siedmiokrotnie rzucamy kostką do gry. Wśród otrzymanych wyników jest 5 czwórek. Jakie jest prawdopodobieństwo, że w pierwszym rzucie otrzymaliśmy czwórkę?
Wyznacz wzór funkcji kwadratowej 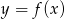 wiedząc, że jest on styczny do prostej
wiedząc, że jest on styczny do prostej 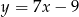 w punkcie
w punkcie 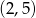 oraz przechodzi przez punkt
oraz przechodzi przez punkt 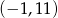 .
.
Rozpatrujemy wszystkie liczby naturalne ośmiocyfrowe, w zapisie których mogą występować wyłącznie cyfry 0, 1, 2, 3 przy czym każda z cyfr występuje dokładnie dwa razy. Ile jest takich liczb?
Rozwiąż równanie 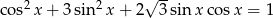 w przedziale
w przedziale 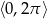 .
.
Wierzchołki 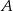 i
i 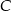 kwadratu
kwadratu 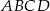 o polu 8 leżą na prostej o równaniu
o polu 8 leżą na prostej o równaniu 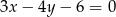 . Środek symetrii tego kwadratu ma współrzędne
. Środek symetrii tego kwadratu ma współrzędne 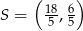 . Oblicz współrzędne punktów
. Oblicz współrzędne punktów 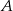 i
i 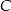 .
.
Wyznacz sinusy kątów ostrych trójkąta prostokątnego wiedząc, że stosunek promieni okręgów opisanego i wpisanego w ten trójkąt jest równy 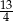 .
.
Dany jest trójmian kwadratowy 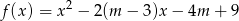 . Wyznacz wszystkie rzeczywiste wartości parametru
. Wyznacz wszystkie rzeczywiste wartości parametru 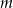 , dla których ten trójmian ma dwa różne pierwiastki
, dla których ten trójmian ma dwa różne pierwiastki 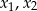 tego samego znaku, spełniające warunek
tego samego znaku, spełniające warunek 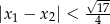 .
.
W ostrosłupie prawidłowym trójkątnym 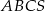 o podstawie
o podstawie 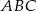 wysokość jest równa 3, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę
wysokość jest równa 3, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę 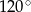 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Rozpatrujemy wszystkie stożki, których pole powierzchni całkowitej jest równe 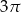 . Oblicz promień podstawy tego stożka, który ma największą objętość. Podaj tę największą objętość.
. Oblicz promień podstawy tego stożka, który ma największą objętość. Podaj tę największą objętość.

