/Szkoła średnia/Zadania maturalne/Matura 2017/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 29 kwietnia 2017 Czas pracy: 180 minut
Zadania zamknięte
Jeżeli 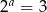 ,
, 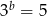 i
i 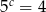 , to iloczyn
, to iloczyn 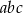 jest równy
jest równy
A) 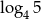 B)
B) 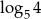 C) 4 D) 2
C) 4 D) 2
Ewa i Kasia rzucają śnieżkami do celu. Ewa trafia do celu średnio raz na pięć rzutów, a Kasia trafia do celu średnio trzy razy na dziesięć rzutów. Prawdopodobieństwo, że cel zostanie trafiony dokładnie raz, jeżeli każda z dziewcząt wykona po jednym rzucie jest równe
A) 0,5 B) 0,56 C) 0,38 D) 0,06
Wielomian 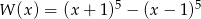 zapisano w postaci
zapisano w postaci 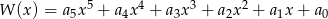 . Suma
. Suma 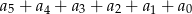 jest równa
jest równa
A) 32 B) 0 C) 1 D) 2
Która z poniższych funkcji nie ma ekstremów lokalnych?
A) 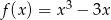 B)
B) 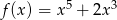 C)
C) 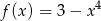 D)
D) 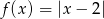
Dla której z podanych funkcji granica prawostronna 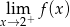 jest skończona?
jest skończona?
A) 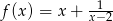 B)
B) 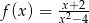 C)
C) 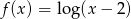 D)
D) 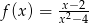
Zadania otwarte
Na płaszczyźnie dany jest nieskończony ciąg 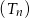 , dla
, dla 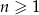 , trójkątów równobocznych. Pole trójkąta
, trójkątów równobocznych. Pole trójkąta 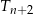 jest dwa razy mniejsze od pola trójkąta
jest dwa razy mniejsze od pola trójkąta 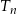 dla
dla 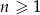 . Uzasadnij, że suma pól trójkątów
. Uzasadnij, że suma pól trójkątów 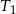 i
i 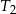 jest równa sumie pól wszystkich pozostałych trójkątów.
jest równa sumie pól wszystkich pozostałych trójkątów.
Funkcja 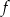 jest określona wzorem
jest określona wzorem 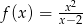 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 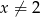 . Oblicz pochodną funkcji
. Oblicz pochodną funkcji 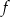 w punkcie
w punkcie 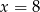 .
.
Liczby niezerowe 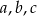 są wyrazami ciągu geometrycznego o numerach odpowiednio
są wyrazami ciągu geometrycznego o numerach odpowiednio 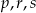 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia
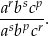
Udowodnij, że średnica okręgu wpisanego w trapez równoramienny, ma długość równą średniej geometrycznej długości podstaw trapezu.
Oblicz miarę kąta ostrego pod jakim przecinają się styczne do wykresu funkcji
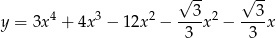
poprowadzone w punktach o pierwszych współrzędnych równych 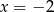 i
i 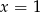 .
.
Uzasadnij, że jeżeli liczby niezerowe 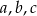 spełniają warunek
spełniają warunek 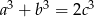 to
to
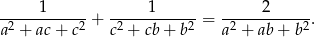
Rozwiąż nierówność 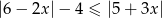 .
.
Napisz równanie okręgu, który jest styczny do prostej 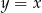 w punkcie
w punkcie 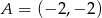 , oraz który odcina z prostej
, oraz który odcina z prostej 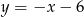 cięciwę o długości 8.
cięciwę o długości 8.
Rozwiąż równanie 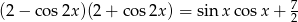 w przedziale
w przedziale 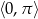 .
.
Dany jest ostrosłup prawidłowy czworokątny 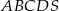 o podstawie
o podstawie 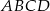 . Pole trójkąta
. Pole trójkąta 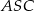 jest równe 120, a cosinus kąta
jest równe 120, a cosinus kąta 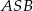 jest równy
jest równy 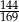 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
Na wykresie funkcji 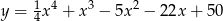 znajdź współrzędne punktu
znajdź współrzędne punktu 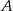 , którego odległość od prostej o równaniu
, którego odległość od prostej o równaniu 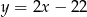 jest najmniejsza.
jest najmniejsza.

