/Szkoła średnia/Zadania maturalne/Matura 2017/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 22 kwietnia 2017 Czas pracy: 170 minut
Zadania zamknięte
Liczba 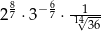 jest równa
jest równa
A) 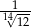 B)
B) 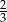 C) 6 D)
C) 6 D) 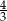
Liczba 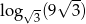 jest równa
jest równa
A) 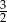 B) 5 C)
B) 5 C) 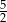 D) 3
D) 3
Dany jest trójkąt o bokach długości 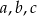 . Stosunek
. Stosunek 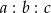 jest równy 3:5:7. Które zdanie jest fałszywe?
jest równy 3:5:7. Które zdanie jest fałszywe?
A) Liczba  jest o 12,5% mniejsza od liczby
jest o 12,5% mniejsza od liczby 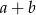
B) Liczba  stanowi 20% liczby
stanowi 20% liczby 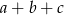
C) Liczba  stanowi 25% liczby
stanowi 25% liczby 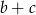
D) Liczba 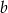 to 60% liczby
to 60% liczby  .
.
Na tablicy zapisano liczby 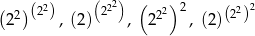 . Ile różnych liczb reprezentują te zapisy?
. Ile różnych liczb reprezentują te zapisy?
A) 4 B) 3 C) 2 D) 1
Wyrażenie 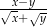 jest równe
jest równe
A) 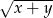 B)
B) 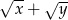 C)
C) 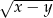 D)
D) 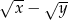
Proste o równaniach 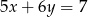 i
i 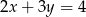 przecinają się w punkcie
przecinają się w punkcie 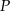 . Stąd wynika, że
. Stąd wynika, że
A) 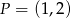 B)
B) 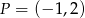 C)
C) 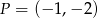 D)
D) 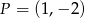
Spośród liczb, które są rozwiązaniami równania 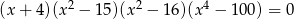 , wybrano największą i najmniejszą. Suma tych dwóch liczb jest liczbą
, wybrano największą i najmniejszą. Suma tych dwóch liczb jest liczbą
A) ujemną B) całkowitą C) niewymierną D) większą od 100
W ciągu arytmetycznym 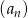 określonym dla
określonym dla 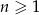 , średnia arytmetyczna trzech pierwszych wyrazów jest dwa razy większa od wyrazu czwartego. Szósty wyraz tego ciągu jest równy
, średnia arytmetyczna trzech pierwszych wyrazów jest dwa razy większa od wyrazu czwartego. Szósty wyraz tego ciągu jest równy
A) 2 B) 0 C) 4 D) 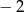
Kąt  jest ostry i
jest ostry i 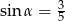 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 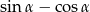 jest równa
jest równa
A) 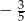 B)
B) 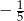 C)
C) 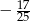 D)
D) 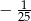
Informacja do zadań 10 i 11
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 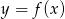 .
.
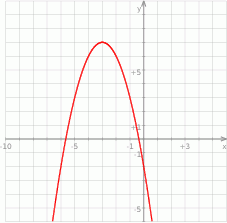
Zbiorem wartości funkcji 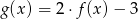 jest przedział
jest przedział
A) 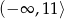 B)
B) 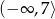 C)
C) 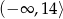 D)
D) 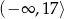
Największa wartość funkcji 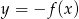 w przedziale
w przedziale 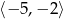 jest równa
jest równa
A) 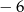 B)
B) 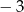 C) 7 D)
C) 7 D) 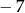
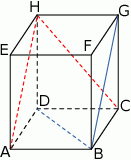
Podstawą graniastosłupa prostego czworokątnego 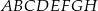 jest kwadrat
jest kwadrat 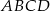 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 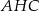 między przekątnymi sąsiednich ścian bocznych ma miarę
między przekątnymi sąsiednich ścian bocznych ma miarę 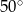 . Kąt
. Kąt 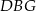 między przekątną podstawy, a przekątną ściany bocznej ma miarę
między przekątną podstawy, a przekątną ściany bocznej ma miarę
A) 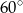 B)
B) 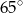 C)
C) 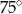 D)
D) 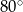
Liczba 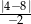 jest równa
jest równa
A) 2 B) 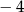 C) 0 D)
C) 0 D) 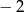
Dziedziną funkcji 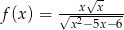 jest
jest
A) 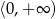 B)
B) 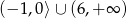 C)
C) 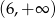 D)
D) 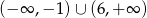
Ciąg 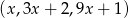 jest geometryczny. Pierwszy wyraz tego ciągu jest równy
jest geometryczny. Pierwszy wyraz tego ciągu jest równy
A) 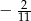 B)
B) 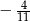 C)
C) 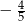 D)
D) 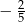
Pole prostokąta, którego boki mają długości 0,002 mm i 500 km jest równe
A) 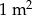 B)
B) 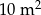 C)
C) 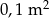 D)
D) 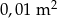
Punkty 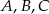 i
i 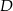 leżą na okręgu o środku
leżą na okręgu o środku 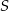 . Cięciwa
. Cięciwa 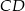 przecina średnicę
przecina średnicę 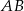 tego okręgu w punkcie
tego okręgu w punkcie 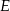 tak, że
tak, że 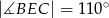 . Kąt środkowy
. Kąt środkowy 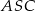 ma miarę
ma miarę 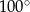 (zobacz rysunek).
(zobacz rysunek).
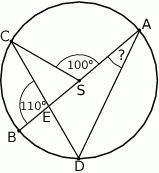
Kąt wpisany 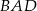 ma miarę
ma miarę
A) 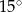 B)
B) 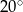 C)
C) 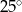 D)
D) 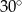
Do pewnej liczby  dodano 65. Otrzymaną sumę podzielono przez 2. W wyniku tego działania otrzymano liczbę trzy razy większą od liczby
dodano 65. Otrzymaną sumę podzielono przez 2. W wyniku tego działania otrzymano liczbę trzy razy większą od liczby  . Zatem
. Zatem
A) 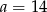 B)
B) 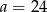 C)
C) 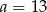 D)
D) 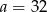
Okręgi o promieniach 3 i 4 są styczne zewnętrznie. Prosta 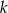 jest styczna do okręgu o promieniu 3 w punkcie
jest styczna do okręgu o promieniu 3 w punkcie 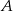 i jest styczna do okręgu o promieniu 4 w punkcie
i jest styczna do okręgu o promieniu 4 w punkcie 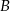 (zobacz rysunek).
(zobacz rysunek).
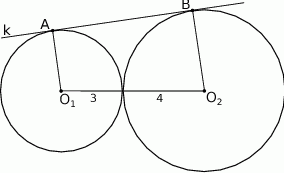
Długość odcinka 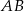 jest równa
jest równa
A) 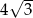 B) 7 C) 6 D)
B) 7 C) 6 D) 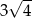
Przekątne równoległoboku mają długości 4 i 8, a kąt między tymi przekątnymi ma miarę 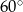 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 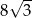 B)
B) 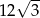 C)
C) 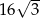 D)
D) 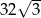
Doświadczenie losowe polega na rzucie trzema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo zdarzenia polegającego na tym, że liczba oczek otrzymanych na kostce jest równa liczbie wylosowanych orłów na monetach jest równe
A) 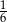 B)
B) 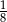 C)
C) 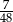 D)
D) 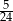
Średnia arytmetyczna liczb: 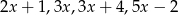 i
i 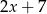 zwiększa się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
zwiększa się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
A) 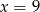 B)
B) 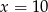 C)
C) 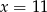 D)
D) 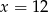
Kąt rozwarcia stożka ma miarę 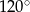 , a wysokość tego stożka ma długość 3. Objętość tego stożka jest równa
, a wysokość tego stożka ma długość 3. Objętość tego stożka jest równa
A) 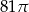 B)
B) 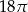 C)
C) 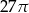 D)
D) 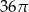
Różnica liczby krawędzi i liczby wierzchołków ostrosłupa jest równa 10. Podstawą tego ostrosłupa jest
A) dziesięciokąt. B) jedenastokąt. C) dwunastokąt. D) trzynastokąt.
Zadania otwarte
Rozwiąż nierówność 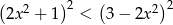 .
.
Jeżeli do licznika pewnego nieskracalnego ułamka dodamy 45, a mianownik pozostawimy niezmieniony, to otrzymamy liczbę 2. Jeżeli natomiast od licznika i od mianownika tego ułamka odejmiemy 3, to otrzymamy liczbę 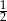 . Wyznacz ten ułamek.
. Wyznacz ten ułamek.
Wiedząc, że 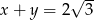 i
i 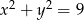 oblicz
oblicz 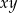 .
.
Dwie proste mają tę własności, że różnica współczynnika kierunkowego i jego odwrotności w przypadku każdej z tych prostych jest taka sama. Uzasadnij, że te proste są prostopadłe albo równoległe.
Dany jest trójkąt prostokątny 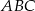 . Na przyprostokątnych
. Na przyprostokątnych 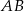 i
i 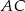 tego trójkąta obrano odpowiednio punkty
tego trójkąta obrano odpowiednio punkty 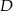 i
i 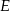 takie, że
takie, że 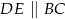 . Na przeciwprostokątnej
. Na przeciwprostokątnej 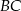 wyznaczono punkt
wyznaczono punkt 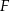 taki, że
taki, że 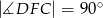 (zobacz rysunek). Wykaż, że trójkąt
(zobacz rysunek). Wykaż, że trójkąt 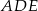 jest podobny do trójkąta
jest podobny do trójkąta 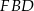 .
.
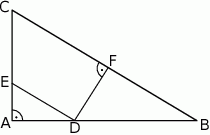
W trójkącie 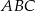 dane są długości boków
dane są długości boków 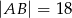 i
i 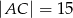 oraz
oraz 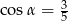 , gdzie
, gdzie 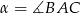 . Na bokach
. Na bokach 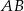 i
i 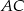 tego trójkąta obrano punkty odpowiednio
tego trójkąta obrano punkty odpowiednio 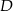 i
i 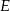 takie, że
takie, że 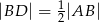 i
i 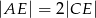 (zobacz rysunek).
(zobacz rysunek).
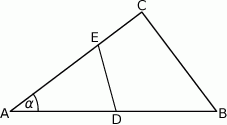
Oblicz pole
- trójkąta
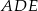 .
. - czworokąta
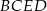 .
.
Ciąg arytmetyczny 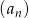 określony jest wzorem
określony jest wzorem 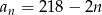 , dla
, dla 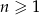 . Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
. Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
Okrąg o środku w punkcie 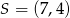 jest styczny do prostej o równaniu
jest styczny do prostej o równaniu 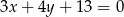 . Oblicz promień tego okręgu oraz współrzędne punktu styczności.
. Oblicz promień tego okręgu oraz współrzędne punktu styczności.
Ze zbioru wszystkich liczb naturalnych trzycyfrowych losujemy kolejno trzy razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie równa 304.

