Zadanie nr 1480099
Wykaż, że jeżeli liczby całkowite 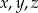 spełniają równanie
spełniają równanie 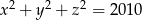 to co najwyżej jedna z liczb
to co najwyżej jedna z liczb 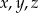 dzieli się przez 4.
dzieli się przez 4.
Rozwiązanie
Sposób I
Gdyby wszystkie trzy liczby dzieliły się przez 4, to 2010 dzieliłoby się przez 4, a łatwo sprawdzić, że się nie dzieli.
Musimy zatem wykluczyć możliwość, że dokładnie dwie z liczb dzielą się przez 4. Przypuśćmy przeciwnie, że np. liczby  i
i 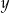 dzielą się, a
dzielą się, a  nie dzieli się przez 4. Zauważmy, że w takiej konfiguracji
nie dzieli się przez 4. Zauważmy, że w takiej konfiguracji  musi być liczbą parzystą (bo inaczej lewa strona równania jest nieparzysta).
musi być liczbą parzystą (bo inaczej lewa strona równania jest nieparzysta).
W takim razie nasze założenia możemy zapisać w postaci
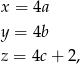
dla pewnych liczb całkowitych 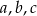 . Podstawiając do danego równania mamy
. Podstawiając do danego równania mamy
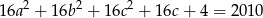
Teraz wystarczy zauważyć, że lewa strona dzieli się przez 4, a prawa nie, co stanowi sprzeczność. W takim razie nie jest możliwe, aby dwie spośród liczb  i
i 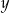 dzieliły się przez 4.
dzieliły się przez 4.
Sposób II
Sprawdźmy jakie reszty z dzielenie przez 4 mogą dawać kwadraty liczb całkowitych.
Jeżeli 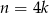 to
to 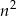 dzieli się przez 4, czyli daje resztę 0.
dzieli się przez 4, czyli daje resztę 0.
Jeżeli 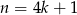 to
to 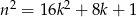 , więc
, więc 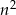 daje resztę 1.
daje resztę 1.
Jeżeli 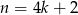 to
to 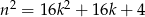 , więc
, więc 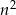 daje resztę 0.
daje resztę 0.
Jeżeli 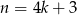 to
to 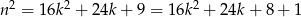 , więc
, więc 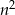 daje resztę 1.
daje resztę 1.
To oznacza, że kwadrat liczby całkowitej zawsze daje resztę 0 lub 1 przy dzieleniu przez 4. Z drugiej strony,
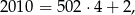
co oznacza, że reszty dokładnie dwóch spośród liczb 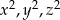 to jedynki, a jedna reszta to 0 (jest to jedyna możliwość, żeby w sumie wyszło 2). To oznacza, że co najwyżej jedna z liczb
to jedynki, a jedna reszta to 0 (jest to jedyna możliwość, żeby w sumie wyszło 2). To oznacza, że co najwyżej jedna z liczb 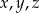 może dzielić się przez 4 (ta której kwadrat daje resztę 0).
może dzielić się przez 4 (ta której kwadrat daje resztę 0).
Uwaga. Można pokazać, że wszystkie naturalne rozwiązania danego równania, w których 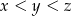 to
to
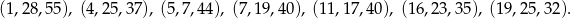
Wszystkie naturalne rozwiązania otrzymamy permutując powyższe trójki, a wszystkie całkowite rozwiązania otrzymamy dodatkowo dowolnie zmieniając znaki liczb 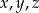 .
.

