Zadanie nr 3112246
Liczby naturalne dodatnie 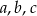 spełniają równanie
spełniają równanie 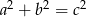 . Uzasadnij, że liczba
. Uzasadnij, że liczba 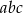 jest
jest
- parzysta;
- podzielna przez 3.
Rozwiązanie
- Jeżeli jedna z liczb
 lub
lub 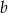 jest parzysta to koniec. Jeżeli natomiast obie są nieparzyste, to parzyste musi być
jest parzysta to koniec. Jeżeli natomiast obie są nieparzyste, to parzyste musi być  jako suma dwóch liczb nieparzystch.
jako suma dwóch liczb nieparzystch. - Sprawdźmy jakie reszty z dzielenia przez 3 może dawać kwadrat
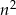 liczby naturalnej. Jeżeli
liczby naturalnej. Jeżeli  dzieli się przez 3, to reszta jest 0. Jeżeli
dzieli się przez 3, to reszta jest 0. Jeżeli 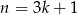 , to mamy
, to mamy 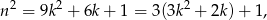
zatem reszta jest 1. Jeżeli natomiast
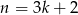 to
to 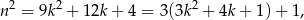
zatem reszta znowu jest 1. Morał z tego taki, że kwadrat liczby naturalnej nie może dawać reszty 2 z dzielenia przez 3.
Jeżeli teraz popatrzymy na równanie
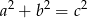
to jedna z liczb
 lub
lub 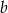 musi dzielić się przez 3. Rzeczywiście, gdyby tak nie było, to lewa strona dawałaby resztę 2 z dzielenia przez 3 (bo kwadrat daje resztę 1), czyli taką samą resztę dawałoby
musi dzielić się przez 3. Rzeczywiście, gdyby tak nie było, to lewa strona dawałaby resztę 2 z dzielenia przez 3 (bo kwadrat daje resztę 1), czyli taką samą resztę dawałoby 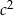 , co, jak już sprawdziliśmy, jest niemożliwe.
, co, jak już sprawdziliśmy, jest niemożliwe.

