/Szkoła średnia/Zadania maturalne/Matura 2017/Matura próbna/CKE, OKE, CEN
Lubelska próba przed maturą
z matematyki poziom rozszerzony 28 lutego 2017 Czas pracy: 180 minut
Zadania zamknięte
Zbiorem wartości funkcji 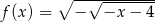 jest
jest
A) 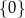 B) zbiór pusty C)
B) zbiór pusty C) 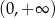 D)
D) 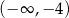
Dziedziną funkcji 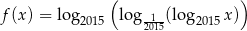 jest przedział
jest przedział
A) 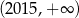 B)
B) 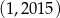 C)
C) 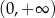 D)
D) 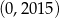
Okrąg o środku w punkcie 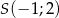 jest styczny do prostej o równaniu
jest styczny do prostej o równaniu 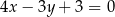 . Promień okręgu jest równy:
. Promień okręgu jest równy:
A)  B) 1 C)
B) 1 C)  D)
D) 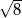
Wycinek kołowy o kącie środkowym 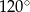 i polu
i polu 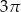 zwinięto w stożek. Promień podstawy tego stożka jest równy:
zwinięto w stożek. Promień podstawy tego stożka jest równy:
A) 2,5 B) 2 C) 1,6 D) 1
W czworościanie foremnym cosinus kąta dwuściennego między dwiema sąsiednimi ścianami jest równy
A) 0 B) 0,25 C) 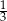 D)
D) 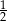
Zadania otwarte
Oblicz granicę 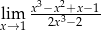 .
.
Udowodnij, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność
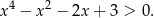
Rozwiąż równanie:

gdzie lewa strona równania jest sumą nieskończonego ciągu geometrycznego.
Dla jakich wartości parametru 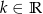 równanie
równanie 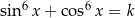 ma rozwiązanie?
ma rozwiązanie?
Oblicz pole trójkąta utworzonego przez osie układu współrzędnych i przez prostą o ujemnym współczynniku kierunkowym 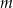 do której należy punkt
do której należy punkt 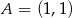 . Dla jakiej wartości
. Dla jakiej wartości 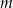 pole tego trójkąta jest najmniejsze?
pole tego trójkąta jest najmniejsze?
W pewnym przedsiębiorstwie 9% wyrobów jest brakami. Na 100 dobrych wyrobów 70 jest pierwszego gatunku. Jakie jest prawdopodobieństwo, że wylosowany wyrób jest pierwszego gatunku?
Wysokość podstawy graniastosłupa prawidłowego trójkątnego ma długość 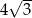 , zaś przekątna ściany bocznej tworzy z krawędzią podstawy kąt równy
, zaś przekątna ściany bocznej tworzy z krawędzią podstawy kąt równy 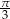 . Graniastosłup ten wpisano w walec. Oblicz pole powierzchni i objętość walca.
. Graniastosłup ten wpisano w walec. Oblicz pole powierzchni i objętość walca.
Dla jakich wartości parametru  równanie
równanie 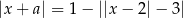 ma dokładnie 2 rozwiązania?
ma dokładnie 2 rozwiązania?
Wyznacz równania wszystkich stycznych do wykresu funkcji 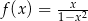 ,
, 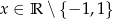 nachylonych do osi
nachylonych do osi 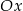 pod kątem
pod kątem 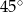 .
.
Dany jest wielomian 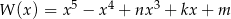 . Wyznacz wszystkie wartości parametrów
. Wyznacz wszystkie wartości parametrów 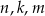 dla których reszta z dzielenia wielomianu
dla których reszta z dzielenia wielomianu 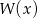 przez wielomian
przez wielomian 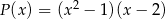 jest równa
jest równa 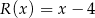 .
.
Dany jest prostokąt 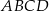 , w którym
, w którym 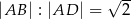 . Punkt
. Punkt 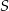 jest środkiem boku
jest środkiem boku 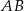 . Oblicz miarę kąta między prostymi
. Oblicz miarę kąta między prostymi 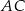 i
i  .
.

