/Szkoła średnia/Zadania maturalne/Matura 2017/Matura próbna/CKE, OKE, CEN
Lubelska próba przed maturą
z matematyki (dla klas drugich)
poziom rozszerzony 2 czerwca 2016 Czas pracy: 180 minut
Zadania zamknięte
Po wykonaniu działania 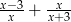 otrzymujemy
otrzymujemy
A) 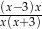 B)
B) 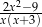 C)
C) 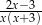 D)
D) 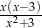
Jeśli 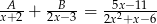 , to suma
, to suma 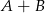 jest równa
jest równa
A) 0 B) 2 C) 1 D) 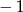
Suma wszystkich pierwiastków wielomianu 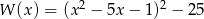 jest równa
jest równa
A) 6 B) 9 C) 10 D) 11
Równanie 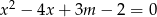 dokładnie jedno rozwiązanie gdy
dokładnie jedno rozwiązanie gdy
A) 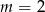 B)
B) 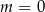 C)
C) 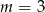 D)
D) 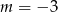
Dany jest ciąg o wyrazie ogólnym 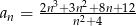 . Suma dwudziestu początkowych wyrazów tego ciągu jest równa
. Suma dwudziestu początkowych wyrazów tego ciągu jest równa
A) 480 B) 380 C) 280 D) 180
Zadania otwarte
Dla jakiej wartości parametru 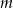 wielomian
wielomian 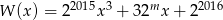 jest podzielny przez dwumian
jest podzielny przez dwumian 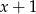 .
.
Podaj wartość wyrażenia 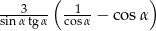 dla
dla 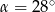 nie używając tablic.
nie używając tablic.
Uzasadnij, że ciąg określony wzorem 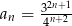 jest ciągiem geometrycznym. Wyznacz iloraz osiemnastego wyrazu tego ciągu przez wyraz 16.
jest ciągiem geometrycznym. Wyznacz iloraz osiemnastego wyrazu tego ciągu przez wyraz 16.
Wyznacz resztę 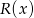 z dzielenia wielomianu
z dzielenia wielomianu 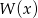 przez wielomian
przez wielomian 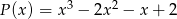 wiedząc, że
wiedząc, że 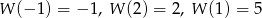 .
.
Trapez prostokątny o podstawach  i
i 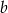 jest opisany na okręgu. Oblicz pole tego trapezu.
jest opisany na okręgu. Oblicz pole tego trapezu.
Wyznacz wszystkie pary liczb całkowitych 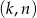 spełniających równość
spełniających równość 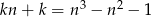 .
.
Dla jakich wartości parametru  układ równań
układ równań 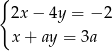 ma rozwiązanie będące parą liczb o różnych znakach?
ma rozwiązanie będące parą liczb o różnych znakach?
Liczby 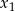 i
i 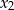 są różnymi od zera rozwiązaniami równania
są różnymi od zera rozwiązaniami równania 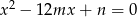 . Liczby
. Liczby 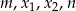 są kolejnymi wyrazami pewnego ciągu geometrycznego. Wyznacz
są kolejnymi wyrazami pewnego ciągu geometrycznego. Wyznacz 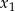 i
i 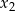 .
.
Naszkicuj wykres funkcji 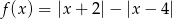 , na podstawie wykresu określ liczbę rozwiązań równania
, na podstawie wykresu określ liczbę rozwiązań równania 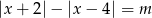 w zależności od parametru
w zależności od parametru 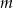 .
.
Dany jest trójkąt równoboczny 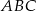 o boku długości 16. Na boku
o boku długości 16. Na boku 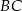 obrano punkt
obrano punkt 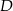 dzielący ten bok w stosunku 3:5, licząc od punktu
dzielący ten bok w stosunku 3:5, licząc od punktu 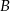 . Oblicz sinus kąta
. Oblicz sinus kąta 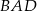 .
.
Punkty 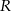 i
i 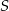 są środkami boków odpowiednio
są środkami boków odpowiednio 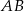 i
i 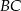 równoległoboku
równoległoboku 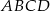 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 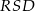 jest równe
jest równe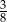 pola tego równoległoboku.
pola tego równoległoboku.

