/Szkoła średnia/Zadania maturalne/Matura 2017/Matura próbna/CKE, OKE, CEN
Próbny Egzamin Maturalny
z Matematyki (CEN Bydgoszcz)
poziom podstawowy 3 marca 2017 Czas pracy: 170 minut
Zadania zamknięte
Pewien towar kosztował 600 zł. Jego cenę obniżono o 15%, a następnie w ramach wyprzedaży sezonowej obniżono o kolejne 10%. Po obu obniżkach towar kosztuje
A) 450 zł B) 459 zł C) 561 zł D) 621 zł
Liczba 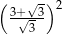 jest równa
jest równa
A) 4 B) 9 C) 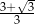 D)
D) 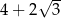
Zbiorem wartości funkcji, której wykres jest przedstawiony na rysunku jest przedział
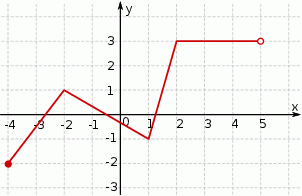
A) 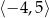 B)
B) 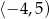 C)
C) 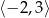 D)
D) 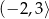
Liczba dodatnich wyrazów ciągu o wyrazie ogólnym 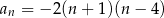 jest równa
jest równa
A) 3 B) 4 C) 5 D) 6
Do prostej należy początek układu współrzędnych oraz punkt 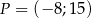 . Wówczas cosinus kąta nachylenia tej prostej do osi
. Wówczas cosinus kąta nachylenia tej prostej do osi 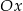 jest równy
jest równy
A) 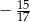 B)
B) 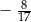 C)
C) 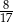 D)
D) 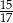
Poniżej przestawiony jest fragment wykresu funkcji kwadratowej. Funkcja ta ma wzór
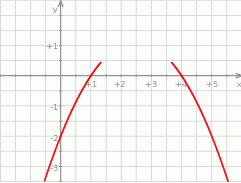
A) 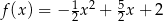 B)
B) 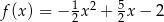
C) 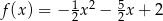 D)
D) 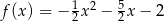
Liczba 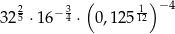 jest równa
jest równa
A) 1 B) 4 C) 64 D) 80
Dana jest prosta 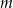 o równaniu
o równaniu 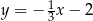 . Prosta
. Prosta 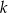 równoległa do prostej
równoległa do prostej 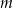 i przechodząca przez punkt
i przechodząca przez punkt 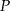 o współrzędnych
o współrzędnych 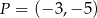 ma równanie
ma równanie
A) 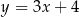 B)
B) 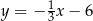 C)
C) 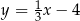 D)
D) 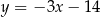
Janek w pierwszym semestrze otrzymał następujące oceny z matematyki: z prac klasowych 2, 3, 3, 4, z kartkówek 5, 5, 4, 4, 5, 5, z odpowiedzi ustnych 2, 3, 4. Oceny z prac klasowych mają wagę 0,5, z kartkówek 0,3, z odpowiedzi ustnych 0,2. Średnia ważona (zaokrąglona do dwóch miejsc po przecinku) ocen z matematyki Janka w pierwszym semestrze jest równa
A) 3,68 B) 3,58 C) 3,25 D) 1,23
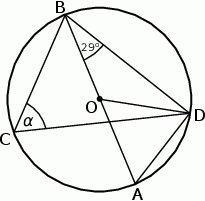
Dany jest kąt  o mierze
o mierze 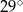 (rys.). Kąt
(rys.). Kąt  ma miarę:
ma miarę:
A) 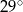 B)
B) 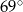 C)
C) 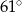 D)
D) 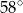
Odległość punktu 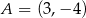 od jego obrazu w symetrii względem początku układu współrzędnych jest równa
od jego obrazu w symetrii względem początku układu współrzędnych jest równa
A) 6 B) 7 C) 8 D) 10
Wartość wyrażenia 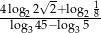 jest równa
jest równa
A)  B) 1 C)
B) 1 C) 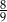 D)
D) 
Suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 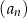 jest wyrażona wzorem
jest wyrażona wzorem 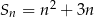 . Drugi wyraz tego ciągu jest równy
. Drugi wyraz tego ciągu jest równy
A) 16 B) 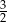 C) 6 D)
C) 6 D) 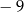
Symetralna odcinka 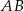 , gdzie
, gdzie 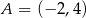 ,
, 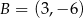 ma równanie
ma równanie
A) 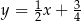 B)
B) 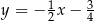 C)
C) 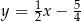 D)
D) 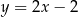
Zbiorem wszystkich rozwiązań równania 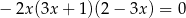 jest
jest
A) 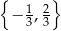 B)
B) 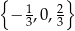 C)
C) 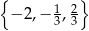 D)
D) 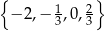
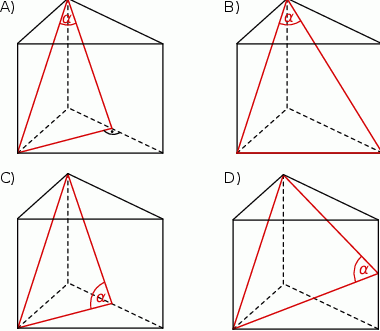
Kąt nachylenia przekątnej ściany bocznej graniastosłupa prawidłowego trójkątnego do sąsiedniej ściany bocznej przedstawiono na rysunku
Do wykresu funkcji liniowej należą punkty 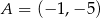 ,
, 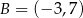 , zatem funkcja liniowa ma wzór
, zatem funkcja liniowa ma wzór
A) 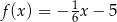 B)
B) 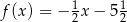 C)
C) 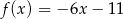 D)
D) 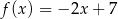
Którym wzorem ogólnym przedstawiono ciąg geometryczny?
A) 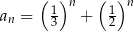 B)
B) 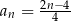 C)
C) 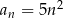 D)
D) 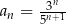
Wartość wyrażenia 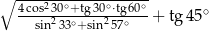 wynosi
wynosi
A) 2 B) 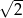 C) 3 D)
C) 3 D) 
Wszystkich liczb naturalnych pięciocyfrowych, w których cyfrą jedności jest 4, cyfra setek jest liczba nieparzystą, a cyfra tysięcy jest liczbą podzielną przez 3 jest
A) 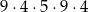 B)
B) 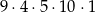 C)
C) 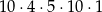 D)
D) 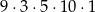
Na rysunkach przedstawione są wykresy funkcji 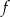 i
i 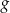 .
.
Wykres funkcji  przekształcono i otrzymano wykres funkcji
przekształcono i otrzymano wykres funkcji  , zatem
, zatem
A) 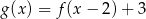 B)
B) 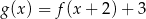
C) 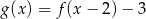 D)
D) 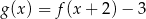
Rozwiązaniem równania 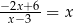 jest
jest
A) 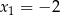 B)
B) 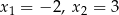 C)
C) 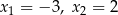 D)
D) 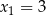
Najmniejsza wartość funkcji kwadratowej 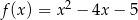 w przedziale
w przedziale 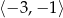 jest równa
jest równa
A) 4 B) 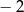 C)
C) 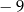 D) 0
D) 0
Zadania otwarte
Na boku 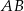 trójkąta równobocznego
trójkąta równobocznego 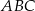 wybrano punkt
wybrano punkt 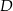 taki, że
taki, że 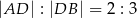 . Oblicz tangens kąta
. Oblicz tangens kąta 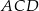 .
.
Rozwiąż nierówność 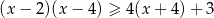 .
.
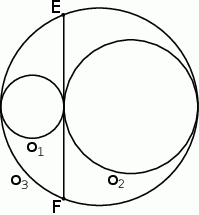
Dane są trzy okręgi 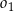 ,
, 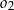 i
i 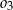 . Okręgi
. Okręgi 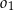 ,
, 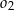 są styczne zewnętrznie, jednocześnie są styczne wewnętrznie do okręgu
są styczne zewnętrznie, jednocześnie są styczne wewnętrznie do okręgu 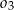 (patrz rysunek). Promienie okręgów
(patrz rysunek). Promienie okręgów 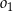 i
i 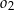 są odpowiednio równe
są odpowiednio równe 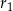 i
i 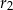 , a środki wszystkich trzech okręgów leżą na jednej prostej. Uzasadnij, że długość odcinka
, a środki wszystkich trzech okręgów leżą na jednej prostej. Uzasadnij, że długość odcinka 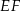 jest równa
jest równa 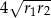 , gdzie odcinek
, gdzie odcinek 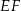 jest cięciwą okręgu
jest cięciwą okręgu  i zawiera się we wspólnej stycznej okręgów
i zawiera się we wspólnej stycznej okręgów  i
i  .
.
Różnica ciągu arytmetycznego jest równa 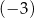 , a szósty wyraz jest równy 3012. Oblicz sumę 2017 początkowych wyrazów tego ciągu.
, a szósty wyraz jest równy 3012. Oblicz sumę 2017 początkowych wyrazów tego ciągu.
Uzasadnij, że suma trzech kolejnych potęg liczby 2 o wykładnikach całkowitych dodatnich jest podzielna przez 14.
Przekątna 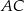 czworokąta
czworokąta 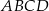 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 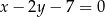 . Wierzchołki
. Wierzchołki 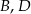 tego czworokąta mają współrzędne
tego czworokąta mają współrzędne 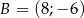 ,
, 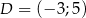 . Oblicz współrzędne punktu przecięcia się przekątnych czworokąta
. Oblicz współrzędne punktu przecięcia się przekątnych czworokąta 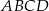 .
.
Ze zbioru liczb 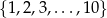 losujemy bez zwracania dwie i od pierwszej odejmujemy drugą. Oblicz prawdopodobieństwo, że otrzymana różnica jest większa od 2.
losujemy bez zwracania dwie i od pierwszej odejmujemy drugą. Oblicz prawdopodobieństwo, że otrzymana różnica jest większa od 2.
Oblicz pole i obwód trapezu prostokątnego, w którym podstawy mają długości 13 cm i 22 cm, a tangens kąta ostrego jest równy 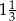 .
.
W ciągu geometrycznym 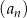 dane są iloraz
dane są iloraz 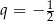 oraz suma
oraz suma
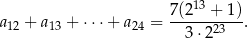
Oblicz  , dla którego ciąg
, dla którego ciąg 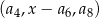 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym.
Suma długości wszystkich krawędzi ostrosłupa prawidłowego trójkątnego jest równa 96, a krawędź boczna tworzy z płaszczyzną podstawy kąt, którego cosinus jest równy 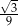 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.

