Zadanie nr 4039007
Dany jest trapez 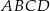 o podstawach
o podstawach 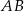 i
i 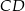 , w którym
, w którym 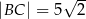 . Okrąg opisany na trójkącie
. Okrąg opisany na trójkącie 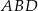 przecina prostą
przecina prostą 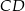 w takim punkcie
w takim punkcie 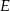 , że
, że 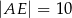 i
i 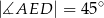 . Oblicz długość podstawy
. Oblicz długość podstawy 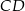 trapezu
trapezu 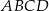 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
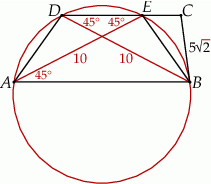
Trapez wpisany w okrąg jest zawsze równoramienny (bo ma oś symetrii), więc 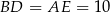 oraz
oraz
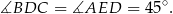
Napiszmy teraz twierdzenie sinusów w trójkącie 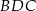 .
.
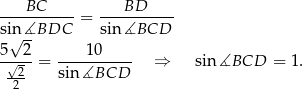
To oznacza, że 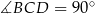 i trójkąt
i trójkąt 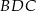 jest połówką kwadratu. Stąd
jest połówką kwadratu. Stąd
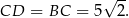
Odpowiedź: 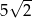 .
.

