/Szkoła średnia/Zadania maturalne/Matura 2017/Matura
Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom rozszerzony 2 czerwca 2017 Czas pracy: 180 minut
Zadania zamknięte
Równanie 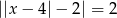 ma dokładnie
ma dokładnie
A) dwa rozwiązania rzeczywiste.
B) jedno rozwiązanie rzeczywiste.
C) cztery rozwiązania rzeczywiste.
D) trzy rozwiązania rzeczywiste.
Liczba 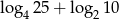 jest równa
jest równa
A) 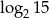 B)
B) 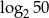 C)
C) 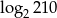 D)
D) 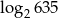
Punkt 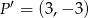 jest obrazem punktu
jest obrazem punktu 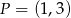 w jednokładności o środku w punkcie
w jednokładności o środku w punkcie 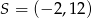 . Skala tej jednokładności jest równa
. Skala tej jednokładności jest równa
A)  B)
B)  C) 2 D) 3
C) 2 D) 3
Funkcja 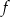 jest określona wzorem
jest określona wzorem 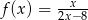 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 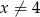 . Wówczas pochodna tej funkcji dla argumentu
. Wówczas pochodna tej funkcji dla argumentu 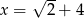 jest równa
jest równa
A) 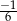 B)
B) 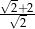 C)
C) 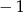 D)
D) 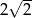
Dany jest nieskończony ciąg geometryczny, w którym iloraz jest trzy razy większy od pierwszego wyrazu, a suma wszystkich wyrazów tego ciągu jest równa 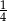 . Pierwszy wyraz tego ciągu jest równy
. Pierwszy wyraz tego ciągu jest równy
A) 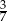 B)
B) 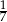 C)
C)  D) 7
D) 7
Zadania otwarte
Funkcja kwadratowa 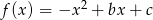 ma dwa miejsca zerowe:
ma dwa miejsca zerowe: 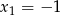 i
i 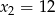 . Oblicz największą wartość tej funkcji.
. Oblicz największą wartość tej funkcji.
Udowodnij, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 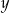 prawdziwa jest nierówność
prawdziwa jest nierówność
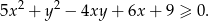
Miary kątów trójkąta 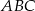 są równe
są równe 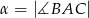 ,
, 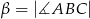 i
i 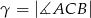 . Punkt
. Punkt 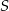 jest środkiem okręgu wpisanego w ten trójkąt, a proste zawierające odcinki
jest środkiem okręgu wpisanego w ten trójkąt, a proste zawierające odcinki 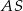 i
i 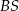 przecinają boki
przecinają boki 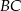 i
i 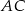 tego trójkąta w punktach odpowiednio
tego trójkąta w punktach odpowiednio 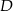 i
i 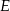 (zobacz rysunek).
(zobacz rysunek).
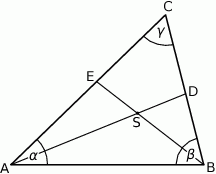
Wykaż, że jeżeli 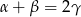 , to na czworokącie
, to na czworokącie 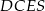 można opisać okrąg.
można opisać okrąg.
Z cyfr 0, 1, 2 tworzymy pięciocyfrowe liczby całkowite dodatnie podzielne przez 15. Oblicz, ile możemy utworzyć takich liczb.
Ciąg 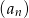 jest arytmetyczny, a ciąg
jest arytmetyczny, a ciąg 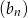 jest geometryczny. Pierwszy wyraz
jest geometryczny. Pierwszy wyraz 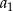 ciągu arytmetycznego jest ilorazem ciągu geometrycznego
ciągu arytmetycznego jest ilorazem ciągu geometrycznego 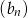 . Wyrazy ciągu
. Wyrazy ciągu 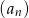 są liczbami całkowitymi, a suma ośmiu początkowych wyrazów tego ciągu jest równa 124. Natomiast pierwszy wyraz
są liczbami całkowitymi, a suma ośmiu początkowych wyrazów tego ciągu jest równa 124. Natomiast pierwszy wyraz 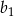 ciągu geometrycznego jest różnicą ciągu arytmetycznego
ciągu geometrycznego jest różnicą ciągu arytmetycznego 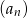 . Suma dwóch pierwszych wyrazów ciągu geometrycznego
. Suma dwóch pierwszych wyrazów ciągu geometrycznego 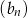 jest równa 18. Wyznacz te ciągi.
jest równa 18. Wyznacz te ciągi.
Rozwiąż równanie 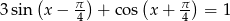 w przedziale
w przedziale 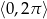 .
.
Prosta 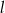 , na której leży punkt
, na której leży punkt 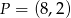 , tworzy z dodatnimi półosiami układu współrzędnych trójkąt prostokątny o polu równym 36. Wyznacz równanie prostej
, tworzy z dodatnimi półosiami układu współrzędnych trójkąt prostokątny o polu równym 36. Wyznacz równanie prostej 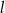 .
.
Wyznacz wszystkie wartości parametru 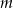 , dla których równanie
, dla których równanie 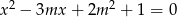 ma dwa różne rozwiązania takie, że każde należy do przedziału
ma dwa różne rozwiązania takie, że każde należy do przedziału 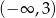 .
.
Trapez równoramienny 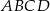 o ramieniu długości 6 wpisany jest w okrąg, przy czym dłuższa podstawa
o ramieniu długości 6 wpisany jest w okrąg, przy czym dłuższa podstawa 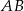 trapezu, o długości 12, jest średnicą tego okręgu. Przekątne
trapezu, o długości 12, jest średnicą tego okręgu. Przekątne 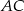 i
i 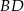 trapezu przecinają się w punkcie
trapezu przecinają się w punkcie 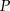 . Oblicz pole koła wpisanego w trójkąt
. Oblicz pole koła wpisanego w trójkąt 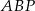 .
.
Rozpatrujemy wszystkie prostopadłościany o objętości 8, których stosunek długości dwóch krawędzi wychodzących z tego samego wierzchołka jest równy 1:2 oraz suma długości wszystkich dwunastu krawędzi jest mniejsza od 28. Wyznacz pole powierzchni całkowitej prostopadłościanu jako funkcję długości jednej z jego krawędzi. Wyznacz dziedzinę tej funkcji. Oblicz wymiary tego spośród rozpatrywanych prostopadłościanów, którego pole powierzchni całkowitej jest najmniejsze.

