/Szkoła średnia/Zadania maturalne/Matura 2018
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 28 kwietnia 2018 Czas pracy: 180 minut
Zadania zamknięte
Liczba 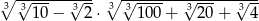 jest równa
jest równa
A) 2 B) 8 C) 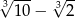 D)
D) 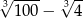
Liczba 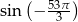 jest równa
jest równa
A) 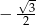 B)
B) 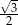 C)
C) 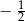 D)
D) 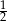
Punkt 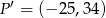 jest obrazem punktu
jest obrazem punktu 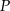 w jednokładności o środku w punkcie
w jednokładności o środku w punkcie 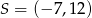 i skali
i skali 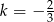 . Współrzędne punktu
. Współrzędne punktu 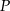 są równe
są równe
A) 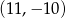 B)
B) 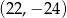 C)
C) 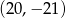 D)
D) 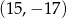
Prosta 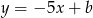 jest styczna do paraboli określonej wzorem
jest styczna do paraboli określonej wzorem 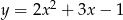 . Liczba
. Liczba 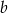 jest równa
jest równa
A) 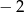 B) 1 C)
B) 1 C) 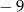 D) 11
D) 11
Wiadomo, że funkcja 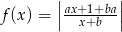 jest funkcją rosnącą w przedziałach
jest funkcją rosnącą w przedziałach 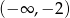 i
i 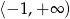 oraz jest funkcją malejącą w przedziale
oraz jest funkcją malejącą w przedziale 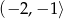 . Zatem
. Zatem
A) 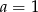 B)
B) 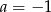 C)
C) 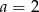 D)
D) 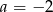
Zadania otwarte
Reszta z dzielenia wielomianu 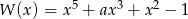 przez dwumian
przez dwumian 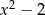 jest równa 1. Oblicz wartość współczynnika
jest równa 1. Oblicz wartość współczynnika  .
.
Oblicz granicę
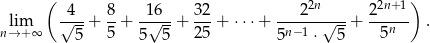
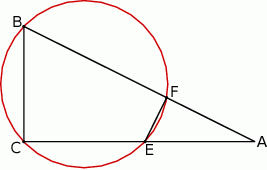
Okrąg przechodzący przez końce przyprostokątnej 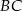 trójkąta prostokątnego
trójkąta prostokątnego 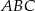 przecina drugą przyprostokątną
przecina drugą przyprostokątną 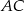 oraz przeciwprostokątną
oraz przeciwprostokątną 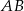 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 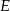 i
i 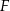 . Wykaż, że promień okręgu opisanego na trójkącie
. Wykaż, że promień okręgu opisanego na trójkącie 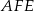 jest równy
jest równy 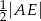 .
.
Oblicz największą wartość wielomianu 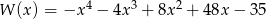 .
.
Wykaż, że jeżeli 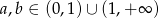 , to
, to
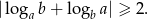
W trójkącie ostrokątnym 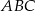 dane są
dane są 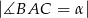 i
i 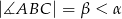 . Wykaż, że tangens kąta utworzonego przez środkową i wysokość opuszczone z wierzchołka
. Wykaż, że tangens kąta utworzonego przez środkową i wysokość opuszczone z wierzchołka 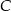 jest równy
jest równy
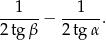
Sześciokrotnie rzucamy kostką do gry. Wśród otrzymanych wyników są dokładnie trzy dwójki. Jakie jest prawdopodobieństwo, że w pierwszym rzucie otrzymaliśmy piątkę?
Czworościan foremny przecięto płaszczyzną 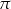 styczną do kuli wpisanej w ten czworościan (tzn. kuli stycznej do wszystkich ścian czworościanu) oraz równoległą do jednej ze ścian czworościanu. Oblicz stosunek objętości brył, na które płaszczyzna
styczną do kuli wpisanej w ten czworościan (tzn. kuli stycznej do wszystkich ścian czworościanu) oraz równoległą do jednej ze ścian czworościanu. Oblicz stosunek objętości brył, na które płaszczyzna 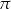 podzieliła czworościan.
podzieliła czworościan.
Rozwiąż równanie 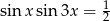 w przedziale
w przedziale 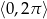 .
.
Wyznacz wszystkie wartości parametru 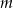 , dla których równanie
, dla których równanie 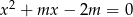 ma dwa różne rozwiązania rzeczywiste
ma dwa różne rozwiązania rzeczywiste 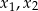 spełniające warunek
spełniające warunek 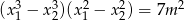 .
.
Wierzchołki czworokąta 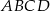 mają współrzędne:
mają współrzędne: 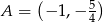 ,
, 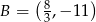 ,
, 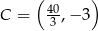 i
i 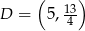 .
.
- Wykaż, że czworokąt
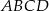 jest trapezem równoramiennym, w który można wpisać okrąg.
jest trapezem równoramiennym, w który można wpisać okrąg. - Wyznacz współrzędne punktu styczności okręgu wpisanego w czworokąt
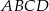 z prostą
z prostą 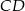 .
.
W ostrosłup prawidłowy czworokątny o wysokości 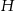 i krawędzi podstawy
i krawędzi podstawy  wpisano walec, którego podstawa zawiera się w podstawie ostrosłupa, i którego oś symetrii pokrywa się z osią symetrii ostrosłupa. Jakie powinny być wymiary tego walca, aby jego objętość była największa możliwa? Oblicz tę największą objętość.
wpisano walec, którego podstawa zawiera się w podstawie ostrosłupa, i którego oś symetrii pokrywa się z osią symetrii ostrosłupa. Jakie powinny być wymiary tego walca, aby jego objętość była największa możliwa? Oblicz tę największą objętość.