/Szkoła średnia/Zadania maturalne/Matura 2018
Egzamin Maturalny
z Matematyki poziom podstawowy 7 maja 2018 Czas pracy: 170 minut
Zadania zamknięte
Liczba 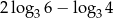 jest równa
jest równa
A) 4 B) 2 C) 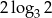 D)
D) 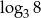
Liczba 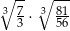 jest równa
jest równa
A) 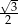 B)
B) 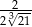 C)
C)  D)
D) 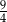
Dane są liczby 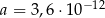 oraz
oraz 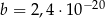 . Wtedy iloraz
. Wtedy iloraz 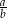 jest równy
jest równy
A) 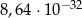 B)
B) 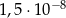 C)
C) 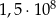 D)
D) 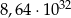
Cena roweru po obniżce o 15% była równa 850 zł. Przed obniżką ten rower kosztował
A) 865,00 zł B) 850,15 zł C) 1000,00 zł D) 977,50 zł
Zbiorem wszystkich rozwiązań nierówności 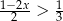 jest przedział
jest przedział
A) 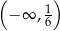 B)
B) 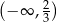 C)
C) 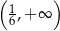 D)
D) 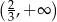
Funkcja kwadratowa jest określona wzorem 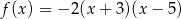 . Liczby
. Liczby 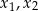 są różnymi miejscami zerowymi funkcji
są różnymi miejscami zerowymi funkcji 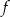 . Zatem
. Zatem
A) 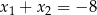 B)
B) 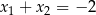 C)
C) 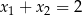 D)
D) 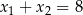
Równanie 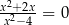
A) ma trzy rozwiązania: 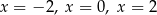
B) ma dwa rozwiązania: 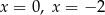
C) ma dwa rozwiązania: 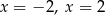
D) ma jedno rozwiązanie: 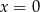
Funkcja liniowa 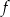 określona jest wzorem
określona jest wzorem 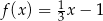 dla wszystkich liczb rzeczywistych
dla wszystkich liczb rzeczywistych  . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe.
A) Funkcja 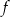 jest malejąca i jej wykres przecina oś
jest malejąca i jej wykres przecina oś 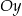 w punkcie
w punkcie 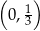
B) Funkcja 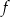 jest malejąca i jej wykres przecina oś
jest malejąca i jej wykres przecina oś 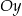 w punkcie
w punkcie 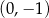
C) Funkcja 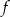 jest rosnąca i jej wykres przecina oś
jest rosnąca i jej wykres przecina oś 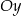 w punkcie
w punkcie 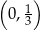
D) Funkcja 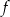 jest rosnąca i jej wykres przecina oś
jest rosnąca i jej wykres przecina oś 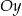 w punkcie
w punkcie 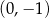
Wykresem funkcji kwadratowej 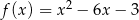 jest parabola, której wierzchołkiem jest punkt o współrzędnych
jest parabola, której wierzchołkiem jest punkt o współrzędnych
A) 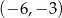 B)
B) 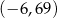 C)
C) 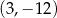 D)
D) 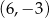
Liczba 1 jest miejscem zerowym funkcji liniowej 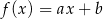 , a punkt
, a punkt 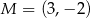 należy do wykresu tej funkcji. Współczynnik
należy do wykresu tej funkcji. Współczynnik  we wzorze tej funkcji jest równy
we wzorze tej funkcji jest równy
A) 1 B)  C)
C) 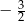 D)
D) 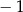
Dany jest ciąg 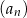 określony wzorem
określony wzorem 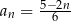 dla
dla 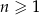 . Ciąg ten jest
. Ciąg ten jest
A) arytmetyczny i jego różnica jest równa 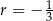 .
.
B) arytmetyczny i jego różnica jest równa 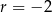 .
.
C) geometryczny i jego iloraz jest równy 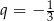 .
.
D) geometryczny i jego iloraz jest równy 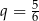 .
.
Dla ciągu arytmetycznego 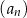 , określonego dla
, określonego dla 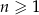 , spełniony jest warunek
, spełniony jest warunek 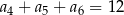 . Wtedy
. Wtedy
A) 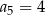 B)
B) 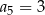 C)
C) 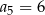 D)
D) 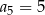
Dany jest ciąg geometryczny 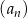 , określony dla
, określony dla 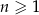 , w którym
, w którym 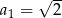 ,
, 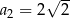 ,
, 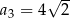 . Wzór na
. Wzór na  -ty wyraz tego ciągu ma postać
-ty wyraz tego ciągu ma postać
A) 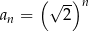 B)
B) 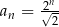 C)
C) 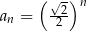 D)
D) 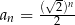
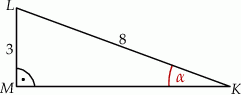
Przyprostokątna 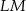 trójkąta prostokątnego
trójkąta prostokątnego 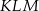 ma długość 3, a przeciwprostokątna
ma długość 3, a przeciwprostokątna 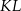 ma długość 8 (zobacz rysunek).
ma długość 8 (zobacz rysunek).
Wtedy miara  kąta ostrego
kąta ostrego 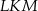 tego trójkąta spełnia warunek
tego trójkąta spełnia warunek
A) 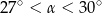 B)
B) 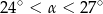 C)
C) 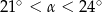 D)
D) 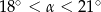
Dany jest trójkąt o bokach długości 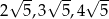 . Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
. Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
A) 10, 15, 20 B) 20, 45, 80 C) 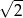 ,
, 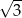 ,
, 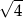 D)
D) 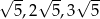
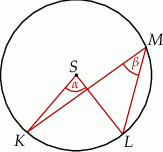
Dany jest okrąg o środku 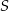 . Punkty
. Punkty 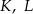 i
i 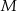 leżą na tym okręgu. Na łuku
leżą na tym okręgu. Na łuku 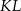 tego okręgu są oparte kąty
tego okręgu są oparte kąty 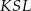 i
i 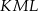 (zobacz rysunek), których miary
(zobacz rysunek), których miary  i
i 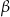 spełniają warunek
spełniają warunek 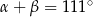 . Wynika stąd, że
. Wynika stąd, że
A) 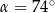 B)
B) 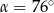 C)
C) 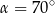 D)
D) 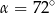
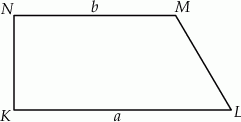
Dany jest trapez prostokątny 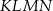 , którego podstawy mają długości
, którego podstawy mają długości 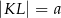 ,
, 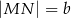 ,
, 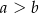 . Kąt
. Kąt 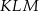 ma miarę
ma miarę 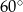 . Długość ramienia
. Długość ramienia 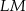 tego trapezu jest równa
tego trapezu jest równa
A) 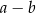 B)
B) 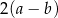 C)
C) 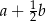 D)
D) 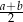
Punkt 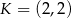 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 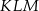 , w którym
, w którym 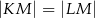 . Odcinek
. Odcinek 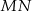 jest wysokością trójkąta i
jest wysokością trójkąta i 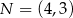 . Zatem
. Zatem
A) 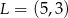 B)
B) 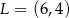 C)
C) 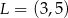 D)
D) 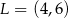
Proste o równaniach 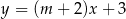 i
i 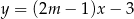 są równoległe, gdy
są równoległe, gdy
A) 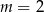 B)
B) 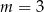 C)
C) 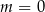 D)
D) 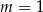
Podstawą ostrosłupa jest kwadrat 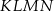 o boku długości 4. Wysokością tego ostrosłupa jest krawędź
o boku długości 4. Wysokością tego ostrosłupa jest krawędź 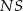 , a jej długość też jest równa 4 (zobacz rysunek).
, a jej długość też jest równa 4 (zobacz rysunek).
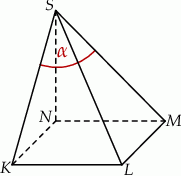
Kąt  , jaki tworzą krawędzie
, jaki tworzą krawędzie 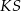 i
i 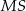 , spełnia warunek
, spełnia warunek
A) 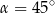 B)
B) 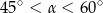 C)
C) 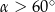 D)
D) 
Podstawą graniastosłupa prostego jest prostokąt o bokach długości 3 i 4. Kąt  , jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy
, jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy 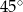 (zobacz rysunek).
(zobacz rysunek).
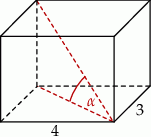
Wysokość graniastosłupa jest równa
A) 5 B) 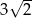 C)
C) 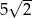 D)
D) 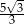
Na rysunku przedstawiono bryłę zbudowaną z walca i półkuli. Wysokość walca jest równa  i jest taka sama jak promień półkuli oraz taka sama jak promień podstawy walca.
i jest taka sama jak promień półkuli oraz taka sama jak promień podstawy walca.
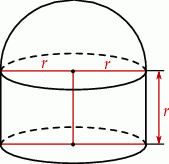
Objętość tej bryły jest równa
A) 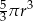 B)
B) 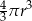 C)
C) 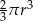 D)
D) 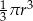
W zestawie 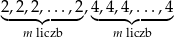 jest
jest 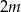 liczb (
liczb (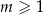 ), w tym
), w tym 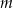 liczb 2 i
liczb 2 i 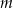 liczb 4. Odchylenie standardowe tego zestawu liczb jest równe
liczb 4. Odchylenie standardowe tego zestawu liczb jest równe
A) 2 B) 1 C) 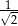 D)
D) 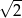
Ile jest wszystkich liczb naturalnych czterocyfrowych mniejszych od 2018 i podzielnych przez 5?
A) 402 B) 403 C) 203 D) 204
W pudełku jest 50 kuponów, wśród których jest 15 kuponów przegrywających, a pozostałe kupony są wygrywające. Z tego pudełka w sposób losowy wyciągamy jeden kupon. Prawdopodobieństwo zdarzenia polegającego na tym, że wyciągniemy kupon wygrywający, jest równe
A) 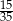 B)
B) 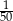 C)
C) 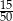 D)
D) 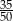
Zadania otwarte
Rozwiąż nierówność 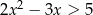 .
.
Rozwiąż równanie 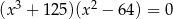 .
.
Udowodnij, że dla dowolnych liczb dodatnich 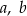 prawdziwa jest nierówność
prawdziwa jest nierówność
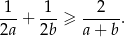
Okręgi o środkach odpowiednio 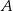 i
i 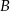 są styczne zewnętrznie i każdy z nich jest styczny do obu ramion danego kąta prostego (zobacz rysunek). Promień okręgu o środku
są styczne zewnętrznie i każdy z nich jest styczny do obu ramion danego kąta prostego (zobacz rysunek). Promień okręgu o środku 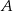 jest równy 2.
jest równy 2.
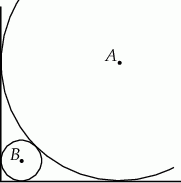
Uzasadnij, że promień okręgu o środku 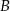 jest mniejszy od
jest mniejszy od 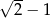 .
.
Do wykresu funkcji wykładniczej, określonej dla każdej liczby rzeczywistej  wzorem
wzorem 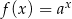 (gdzie
(gdzie 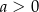 i
i 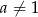 ), należy punkt
), należy punkt 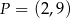 . Oblicz
. Oblicz  i zapisz zbiór wartości funkcji
i zapisz zbiór wartości funkcji 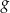 , określonej wzorem
, określonej wzorem 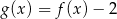 .
.
Dwunasty wyraz ciągu arytmetycznego 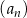 , określonego dla
, określonego dla 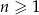 , jest równy 30, a suma jego dwunastu początkowych wyrazów jest równa 162. Oblicz pierwszy wyraz tego ciągu.
, jest równy 30, a suma jego dwunastu początkowych wyrazów jest równa 162. Oblicz pierwszy wyraz tego ciągu.
W układzie współrzędnych punkty 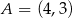 i
i 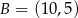 są wierzchołkami trójkąta
są wierzchołkami trójkąta 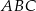 . Wierzchołek
. Wierzchołek 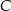 leży na prostej o równaniu
leży na prostej o równaniu 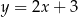 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 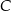 , dla którego kąt
, dla którego kąt 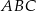 jest prosty.
jest prosty.
Dane są dwa zbiory: 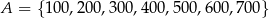 i
i 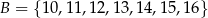 . Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie podzielna przez 3. Obliczone prawdopodobieństwo zapisz w postaci nieskracalnego ułamka zwykłego.
. Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie podzielna przez 3. Obliczone prawdopodobieństwo zapisz w postaci nieskracalnego ułamka zwykłego.
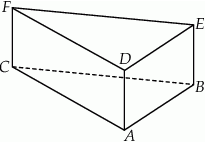
Dany jest graniastosłup prawidłowy trójkątny (zobacz rysunek). Pole powierzchni całkowitej tego graniastosłupa jest równe 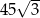 . Pole podstawy graniastosłupa jest równe polu jednej ściany bocznej. Oblicz objętość tego graniastosłupa.
. Pole podstawy graniastosłupa jest równe polu jednej ściany bocznej. Oblicz objętość tego graniastosłupa.