Zadanie nr 2816194
Na budowę domu możesz zaciągnąć pożyczkę w wysokości 63450 €. Do wyboru są dwa warianty spłaty:
I – w każdym miesiącu spłacasz równe raty, każdą w wysokości 2% pożyczonej kwoty.
II – pierwsza rata miesięczna wynosi 2500 €, a każda następna jest o 50 € mniejsza niż poprzednia.
Ile miesięcy potrwa spłata mieszkania w każdym z wariantów?
Rozwiązanie
W I wariancie każda rata wynosi 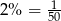 całej kwoty kredytu. Spłata będzie więc trwać 50 miesięcy.
całej kwoty kredytu. Spłata będzie więc trwać 50 miesięcy.
W II wariancie raty zmieniają się jak wyrazy ciągu arytmetycznego o różnicy -50. Po  miesiącach spłaty, suma wszystkich rat będzie więc wynosić (wzór na sumę wyrazów ciągu arytmetycznego)
miesiącach spłaty, suma wszystkich rat będzie więc wynosić (wzór na sumę wyrazów ciągu arytmetycznego)
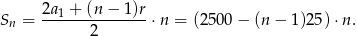
Mamy więc równanie
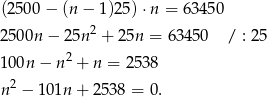
Dalej, 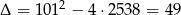 ,
, 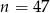 lub
lub 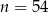 . Zauważmy, że tylko pierwsza z wartości stanowi rozwiązanie – druga z nich odpowiada sytuacji, gdy raty zaczynają być ujemne, co oczywiście nie ma sensu.
. Zauważmy, że tylko pierwsza z wartości stanowi rozwiązanie – druga z nich odpowiada sytuacji, gdy raty zaczynają być ujemne, co oczywiście nie ma sensu.
Odpowiedź: I wariant: 50 miesięcy, II wariant: 47 miesięcy.

