/Szkoła średnia/Zadania maturalne/Matura 2018/Matura próbna
Lubelska próba przed maturą
z matematyki poziom podstawowy grupa II 14 marca 2018 Czas pracy: 170 minut
Zadania zamknięte
Rozwiązaniem układu nierówności 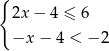 jest zbiór
jest zbiór
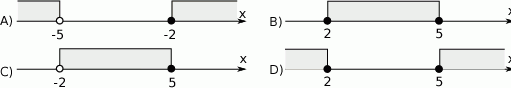
Wartość wyrażenia 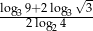 jest równa
jest równa
A) 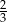 B) 4 C)
B) 4 C) 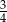 D) 9
D) 9
Cenę towaru obniżano dwa razy. Pierwsza obniżka wynosiła 10%, a druga 20%. O ile procent w wyniku obu obniżek spadła cena towaru?
A) o 24% B) o 28% C) o 26% D) o 30%
Jeżeli 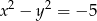 i
i 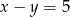 , to wartość wyrażenia
, to wartość wyrażenia 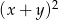 jest równa
jest równa
A) 1 B) 16 C) 9 D) 25
Układ równań 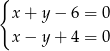 opisuje w układzie współrzędnych na płaszczyźnie punkt
opisuje w układzie współrzędnych na płaszczyźnie punkt
A) 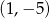 B)
B) 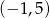 C)
C) 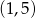 D)
D) 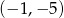
Suma wszystkich pierwiastków równania: 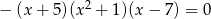 jest równa
jest równa
A) 0 B) 1 C) 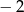 D) 2
D) 2
Rozwiązaniem równania 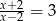 (
(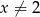 ) jest liczba
) jest liczba
A) 4 B) 3 C) 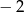 D)
D) 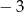
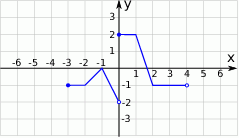
Jeśli na rysunku przedstawiony jest wykres funkcji 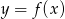 , to dziedziną funkcji
, to dziedziną funkcji  jest zbiór
jest zbiór
A) 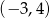 B)
B) 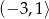 C)
C) 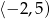 D)
D) 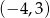
Funkcja liniowa 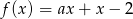 jest malejąca. Wynika stąd, że
jest malejąca. Wynika stąd, że
A) 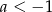 B)
B) 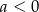 C)
C) 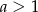 D)
D) 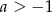
Miejsce zerowe funkcji liniowej 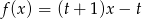 jest równe 2. Wynika stąd, że
jest równe 2. Wynika stąd, że
A) 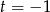 B)
B) 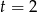 C)
C) 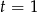 D)
D) 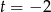
Funkcja kwadratowa określona jest wzorem 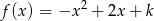 . Jeżeli
. Jeżeli 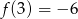 , to
, to
A) 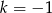 B)
B) 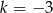 C)
C) 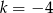 D)
D) 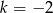
Najmniejszą liczbą całkowitą spełniającą nierówność 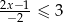 jest
jest
A) 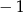 B)
B) 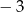 C)
C) 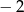 D)
D) 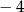
W rosnącym ciągu geometrycznym 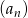 , określonym dla
, określonym dla 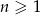 , spełniony jest warunek
, spełniony jest warunek 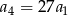 . Iloraz
. Iloraz 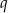 tego ciągu jest równy
tego ciągu jest równy
A) 2 B) 4 C) 3 D) 5
Jeśli 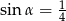 , to długość przyprostokątnej
, to długość przyprostokątnej 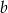 danego trójkąta (patrz rysunek) jest równa
danego trójkąta (patrz rysunek) jest równa
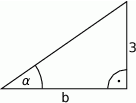
A) 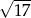 B)
B) 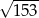 C)
C) 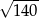 D)
D) 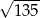
Sinus kąta ostrego  jest równy
jest równy 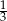 . Wówczas
. Wówczas 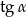 jest równy
jest równy
A) 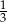 B)
B) 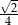 C)
C) 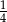 D)
D) 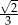
W okręgu o środku 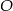 dany jest kąt o mierze
dany jest kąt o mierze 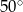 , zaznaczony na rysunku.
, zaznaczony na rysunku.
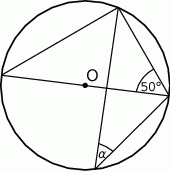
Miara kąta oznaczonego na rysunku literą  jest równa
jest równa
A) 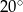 B)
B) 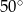 C)
C) 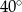 D)
D) 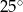
Przekątna prostokąta ma długość 12 cm i tworzy z jednym z boków kąt o mierze 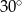 . Pole powierzchni tego prostokąta jest równe
. Pole powierzchni tego prostokąta jest równe
A) 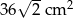 B)
B) 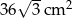 C)
C) 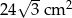 D)
D) 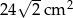
Proste o równaniach 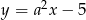 oraz
oraz 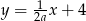 (
(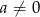 ) są prostopadłe dla
) są prostopadłe dla  równego
równego
A) 1 B) 2 C) 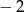 D)
D) 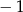
Jeśli suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 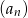 określona jest wzorem
określona jest wzorem 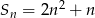 , to wartość trzeciego wyrazu tego ciągu jest równa
, to wartość trzeciego wyrazu tego ciągu jest równa
A) 8 B) 10 C) 21 D) 11
Obrazem punktu 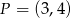 w symetrii środkowej względem punktu
w symetrii środkowej względem punktu 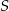 jest punkt
jest punkt 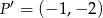 . Wynika stąd, że
. Wynika stąd, że
A) 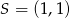 B)
B) 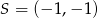 C)
C) 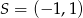 D)
D) 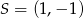
Powierzchnia boczna walca po rozwinięciu jest kwadratem o polu 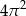 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 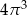 B)
B) 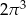 C)
C) 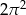 D)
D) 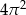
Kula wpisana w sześcian o przekątnej równej 6 ma objętość równą
A) 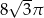 B)
B) 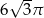 C)
C) 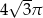 D)
D) 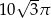
Ile jest wszystkich liczb naturalnych dwucyfrowych, w których obie cyfry są nieparzyste?
A) 16 B) 24 C) 20 D) 25
Uczniowie pewnej klasy zostali poproszeni o odpowiedź na pytanie: „Ile osób liczy twoja rodzina?” Wyniki przedstawiono w tabeli:
| Liczba osób w rodzinie | Liczba uczniów |
| 3 | 6 |
| 4 | 12 |
| x | 2 |
Średnia liczba osób w rodzinie dla uczniów tej klasy jest równa 4. Wtedy liczba x jest równa
A) 7 B) 4 C) 5 D) 3
Ze zbioru kolejnych liczb naturalnych 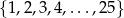 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby, która jest kwadratem liczby całkowitej, jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby, która jest kwadratem liczby całkowitej, jest równe
A) 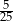 B)
B) 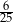 C)
C) 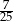 D)
D) 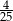
Zadania otwarte
Rozwiąż nierówność 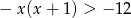 .
.
Wykaż, ze dla dowolnych liczb rzeczywistych 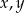 prawdziwa jest nierówność
prawdziwa jest nierówność 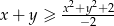 .
.
Uzasadnij, że jeśli miary kątów wewnętrznych pewnego trójkąta są kolejnymi wyrazami ciągu arytmetycznego, to jeden z tych kątów ma miarę 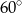 .
.
Funkcja kwadratowa o wzorze 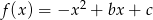 ma dwa miejsca zerowe
ma dwa miejsca zerowe 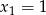 i
i 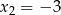 . Wyznacz wartość liczbową współczynników
. Wyznacz wartość liczbową współczynników 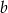 i
i  .
.
Oblicz odległość punktu 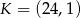 od środka odcinka o końcach
od środka odcinka o końcach 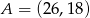 ,
, 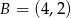 .
.
W pewnej klasie liczba dziewcząt stanowi 60% liczby wszystkich uczniów. Gdyby 6 dziewcząt przeniosło się do innej klasy, w klasie pozostałoby po tyle samo dziewcząt i chłopców. Oblicz ile osób liczy ta klasa oraz ile jest w niej chłopców.
W graniastosłupie czworokątnym prawidłowym przekątna o długości 5 jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 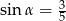 . Wyznacz objętość tego graniastosłupa.
. Wyznacz objętość tego graniastosłupa.
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia 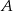 polegającego na tym, że w pierwszym rzucie otrzymamy nieparzystą liczbę oczek i suma liczb oczek w obu rzutach będzie większa od 6. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
polegającego na tym, że w pierwszym rzucie otrzymamy nieparzystą liczbę oczek i suma liczb oczek w obu rzutach będzie większa od 6. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
Trzy liczby, których suma jest równa 52, tworzą ciąg geometryczny. Jeśli pierwszą liczbę zmniejszymy o 16, to otrzymamy ciąg arytmetyczny. Wyznacz te liczby.

