/Szkoła średnia/Zadania maturalne/Matura 2018/Matura próbna
Lubelska próba przed maturą
z matematyki poziom rozszerzony 14 marca 2018 Czas pracy: 180 minut
Zadania zamknięte
Wzór funkcji liniowej, której wykresem jest prosta nachylona do osi 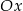 pod kątem o mierze
pod kątem o mierze 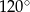 i przechodzi przez punkt
i przechodzi przez punkt 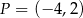 jest postaci
jest postaci
A) 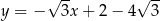 B)
B) 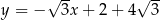
C) 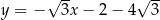 D)
D) 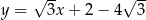
Do okręgu należą punkty 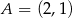 ,
, 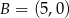 ,
, 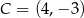 . Jest to okrąg o środku
. Jest to okrąg o środku 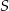 i promieniu
i promieniu  :
:
A) 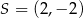 ,
, 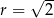 B)
B) 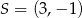 ,
, 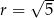
C) 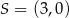 ,
, 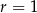 D)
D) 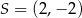 ,
, 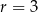
Funkcja 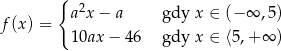 jest ciągła w zbiorze liczb rzeczywistych jeżeli
jest ciągła w zbiorze liczb rzeczywistych jeżeli  jest równe
jest równe
A) 1 lub 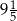 B) 5 lub
B) 5 lub 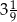 C) 5 lub
C) 5 lub 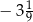 D) 1 lub 5
D) 1 lub 5
Ile różnych wyrazów z sensem lub bez sensu można ułożyć z liter wyrazu: MATEMATYKA?
A) 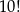 B) 30240 C) 151200 D)
B) 30240 C) 151200 D) 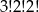
Rozwiązaniem nierówności 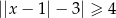 jest
jest
A) 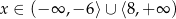 B)
B) 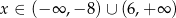 C)
C) 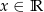 D)
D) 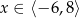
Zadania otwarte
Wyznacz zbiór argumentów, dla których funkcja 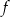 określona wzorem
określona wzorem 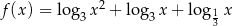 przyjmuje wartości z przedziału
przyjmuje wartości z przedziału 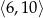 .
.
W rombie 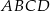 , którego pole jest równe 10 dane są przeciwległe wierzchołki
, którego pole jest równe 10 dane są przeciwległe wierzchołki 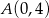 i
i 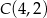 . Wyznacz współrzędne pozostałych wierzchołków rombu.
. Wyznacz współrzędne pozostałych wierzchołków rombu.
Wiadomo, że liczby 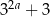 ,
, 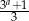 ,
, 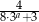 są odpowiednio pierwszym, drugim i trzecim wyrazem nieskończonego ciągu geometrycznego. Wyznacz
są odpowiednio pierwszym, drugim i trzecim wyrazem nieskończonego ciągu geometrycznego. Wyznacz  . Dla wyznaczonej wartości
. Dla wyznaczonej wartości  zapisz wzór tego ciągu i oblicz sumę jego wszystkich wyrazów.
zapisz wzór tego ciągu i oblicz sumę jego wszystkich wyrazów.
Wykaż, że jeśli  , to
, to 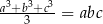 .
.
Wyznacz wszystkie wartości parametru 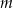 , dla których równanie
, dla których równanie 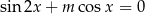 ma w przedziale
ma w przedziale 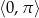 trzy rozwiązania.
trzy rozwiązania.
Dany jest trójkąt prostokątny równoramienny 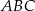 . Punkty
. Punkty 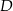 i
i 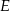 dzielą przeciwprostokątną
dzielą przeciwprostokątną 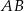 na trzy odcinki równej długości. Oblicz cosinus kąta
na trzy odcinki równej długości. Oblicz cosinus kąta 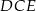 .
.
Dana jest parabola o równaniu 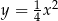 i punkt
i punkt 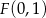 . Wykaż, że każdy punkt leżący na paraboli jest równo oddalony od punktu
. Wykaż, że każdy punkt leżący na paraboli jest równo oddalony od punktu 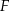 i prostej
i prostej 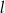 o równaniu
o równaniu 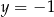 .
.
Wyznacz miejsca zerowe funkcji 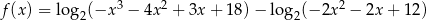 .
.
Punkt 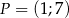 należy do wykresu funkcji
należy do wykresu funkcji 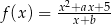 , gdzie
, gdzie 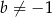 . Styczna do wykresu danej funkcji, poprowadzona w punkcie
. Styczna do wykresu danej funkcji, poprowadzona w punkcie 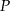 , jest prostopadła do prostej o równaniu
, jest prostopadła do prostej o równaniu 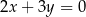 . Oblicz współczynniki
. Oblicz współczynniki  i
i 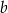 oraz napisz równanie tej stycznej.
oraz napisz równanie tej stycznej.
Ze zbioru 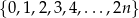 gdzie
gdzie 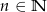 wylosowano jednocześnie 3 liczby. Prawdopodobieństwo, że suma wylosowanych liczb jest nieparzysta wynosi
wylosowano jednocześnie 3 liczby. Prawdopodobieństwo, że suma wylosowanych liczb jest nieparzysta wynosi 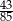 . Wyznacz ile liczb było w zbiorze.
. Wyznacz ile liczb było w zbiorze.
Przekrojem osiowym stożka jest trójkąt o obwodzie 40. Podaj promień podstawy i wysokość stożka o największej objętości. Oblicz jego objętość.

