/Szkoła średnia/Zadania maturalne/Matura 2018/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 5 maja 2018 Czas pracy: 170 minut
Zadania zamknięte
Liczba 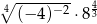 jest równa
jest równa
A) 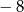 B) 8 C)
B) 8 C) 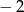 D) 4
D) 4
Liczba 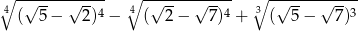 jest równa
jest równa
A) 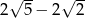 B)
B) 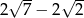 C)
C) 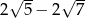 D)
D) 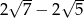
Liczba 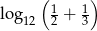 jest równa
jest równa
A) 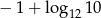 B) 10 C)
B) 10 C) 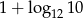 D)
D) 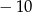
Badając pewien roztwór stwierdzono, że zawiera on 0,05 g chloru, co stanowi 0,02% masy roztworu. Jaka była masa roztworu?
A) 2,5 kg B) 250 g C) 25 g D) 2,5 g
Liczba 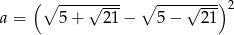 jest równa
jest równa
A) 4 B) 6 C) 10 D) 14
Przedział 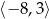 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 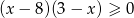
B) 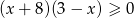
C) 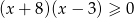
D) 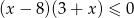
Zbiorem rozwiązań nierówności 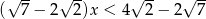 jest przedział
jest przedział
A) 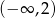 B)
B) 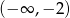 C)
C) 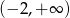 D)
D) 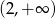
Liczba ujemnych pierwiastków równania 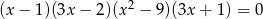 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Funkcja liniowa 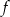 jest określona wzorem
jest określona wzorem 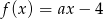 , gdzie
, gdzie 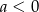 . Wówczas spełniony jest warunek
. Wówczas spełniony jest warunek
A) 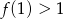 B)
B) 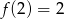 C)
C) 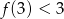 D)
D) 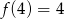
Dane są funkcje 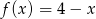 oraz
oraz 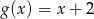 określone dla wszystkich liczb rzeczywistych
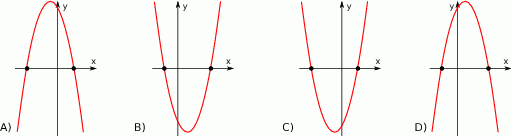
określone dla wszystkich liczb rzeczywistych  . Wskaż, który z poniższych wykresów jest wykresem funkcji
. Wskaż, który z poniższych wykresów jest wykresem funkcji 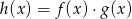 .
.
Ciąg 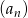 spełnia warunek
spełnia warunek 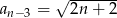 dla
dla 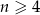 . Wówczas
. Wówczas
A) 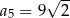 B)
B) 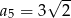 C)
C) 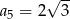 D)
D) 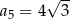
Dwa kolejne wyrazy ciągu geometrycznego 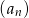 są równe 4 i 24. Wyrazem tego ciągu może być liczba
są równe 4 i 24. Wyrazem tego ciągu może być liczba
A) 96 B) 108 C) 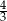 D)
D) 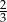
Kąt  jest kątem ostrym i
jest kątem ostrym i 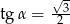 . Jaki warunek spełnia kąt
. Jaki warunek spełnia kąt  ?
?
A) 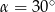 B)
B) 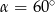 C)
C) 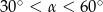 D)
D) 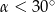
Na rysunku przedstawiony jest wykres funkcji 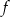 .
.
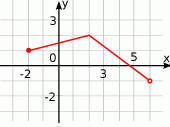
Wykres funkcji 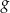 , określonej wzorem
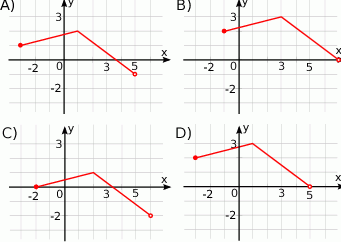
, określonej wzorem 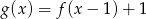 , przedstawia rysunek:
, przedstawia rysunek:
Punkty 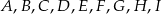 dzielą okrąg na 9 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego
dzielą okrąg na 9 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego 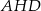 jest równa
jest równa
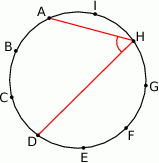
A) 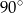 B)
B) 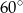 C)
C) 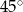 D)
D) 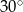
Pięciokąt 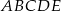 jest foremny. Wskaż trójkąt podobny do trójkąta
jest foremny. Wskaż trójkąt podobny do trójkąta 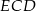
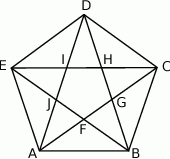
A) 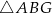 B)
B) 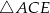 C)
C) 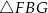 D)
D) 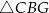
Pole prostokąta przedstawionego na rysunku jest równe 18. Zatem
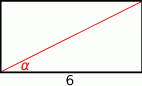
A) 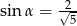 B)
B) 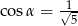 C)
C) 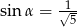 D)
D) 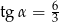
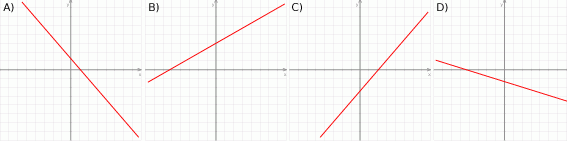
Na którym rysunku przedstawiono wykres funkcji liniowej 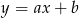 takiej, że
takiej, że 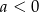 i
i 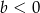 ?
?
Prosta 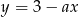 jest równoległa do prostej
jest równoległa do prostej 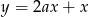 . Wtedy
. Wtedy
A) 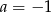 B)
B) 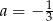 C)
C) 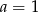 D)
D) 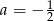
Punkt 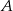 ma współrzędne
ma współrzędne 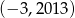 . Punkt
. Punkt 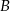 jest symetryczny do punktu
jest symetryczny do punktu 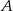 względem osi
względem osi 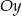 , a punkt
, a punkt 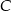 jest symetryczny do punktu
jest symetryczny do punktu 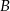 względem osi
względem osi 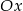 . Punkt
. Punkt 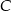 ma współrzędne
ma współrzędne
A) 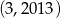 B)
B) 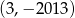 C)
C) 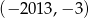 D)
D) 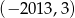
Trójkąt prostokątny o przyprostokątnych 4 i 6 obracamy wokół krótszej przyprostokątnej. Objętość powstałego stożka jest równa:
A) 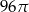 B)
B) 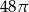 C)
C) 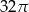 D)
D) 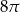
Przekrój osiowy walca jest kwadratem o boku  . Jeżeli
. Jeżeli 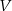 oznacza objętość walca,
oznacza objętość walca, 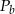 oznacza pole powierzchni bocznej walca, to
oznacza pole powierzchni bocznej walca, to
A) 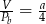 B)
B) 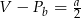 C)
C) 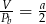 D)
D) 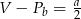
Objętość kuli stycznej do wszystkich ścian sześcianu o krawędzi długości 18 jest równa
A) 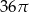 B)
B) 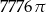 C)
C) 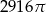 D)
D) 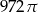
Wiadomo, że mediana liczb 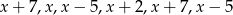 jest równa średniej tych liczb. Zatem liczba
jest równa średniej tych liczb. Zatem liczba 
A) jest równa 3 B) jest równa 4 C) jest równa 5 D) może mieć dowolną wartość
Pan Henryk szykując się rano do pracy wybiera jeden spośród swoich 10 zegarków oraz dwa spośród 18 wiecznych piór, przy czym jedno z nich traktuje jako pióro zapasowe. Na ile sposobów może wybrać zestaw składający się z zegarka i dwóch piór, głównego i zapasowego?
A) 45 B) 46 C) 3240 D) 3060
Zadania otwarte
Rozwiąż nierówność 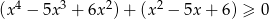 .
.
Wykaż, że reszta z dzielenia sumy kwadratów czterech kolejnych liczb naturalnych przez 4 jest równa 2.
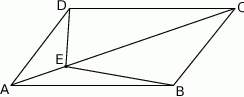
Na przekątnej 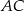 równoległoboku
równoległoboku 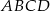 wybrano punkt
wybrano punkt 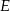 (zobacz rysunek). Uzasadnij, że trójkąty
(zobacz rysunek). Uzasadnij, że trójkąty 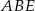 i
i 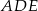 mają równe pola.
mają równe pola.
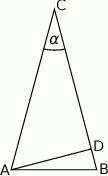
W trójkącie równoramiennym 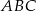 dane są
dane są 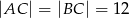 i
i 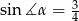 (zobacz rysunek). Oblicz wysokość
(zobacz rysunek). Oblicz wysokość 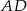 trójkąta opuszczoną z wierzchołka
trójkąta opuszczoną z wierzchołka 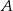 na bok
na bok 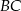 .
.
Czwarty wyraz ciągu arytmetycznego jest równy 8. Suma pięciu pierwszych wyrazów tego ciągu jest równa 15. Oblicz siódmy wyraz tego ciągu.
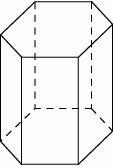
Spośród wierzchołków graniastosłupa sześciokątnego prostego losujemy jeden wierzchołek z dolnej podstawy i jeden wierzchołek z górnej podstawy. Oblicz prawdopodobieństwo tego, że wylosowane wierzchołki są końcami krawędzi bocznej graniastosłupa.
Zosia wrzucała do rzeki kamyki, przy czym w sumie wrzuciła 36 kamyków. Gdyby wrzucała kamyki ze średnią częstością o 20% większą, to czas potrzebny na wrzucenie wszystkich kamyków skróciłby się o 12 sekund. Oblicz, ile średnio kamyków na sekundę wrzucała Zosia do rzeki.
Dany jest kwadrat 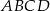 o polu 10 i wierzchołku
o polu 10 i wierzchołku 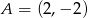 . Przekątna
. Przekątna 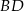 tego kwadratu ma równanie
tego kwadratu ma równanie 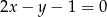 . Oblicz współrzędne pozostałych wierzchołków kwadratu.
. Oblicz współrzędne pozostałych wierzchołków kwadratu.
Punkty 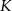 i
i 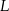 są środkami krawędzi
są środkami krawędzi 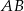 i
i 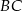 sześcianu
sześcianu 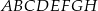 o krawędzi długości 1. Punkt
o krawędzi długości 1. Punkt 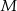 jest środkiem ściany
jest środkiem ściany 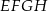 (zobacz rysunek). Oblicz pole trójkąta
(zobacz rysunek). Oblicz pole trójkąta 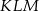 .
.