/Szkoła średnia/Zadania maturalne/Matura 2018/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 21 kwietnia 2018 Czas pracy: 170 minut
Zadania zamknięte
Liczba 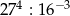 jest równa
jest równa
A) 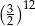 B)
B) 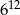 C)
C) 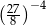 D)
D) 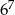
Iloczyn dodatnich liczb 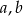 i
i  jest równy 6048. Ponadto 9% liczby
jest równy 6048. Ponadto 9% liczby  jest równe 8% liczby
jest równe 8% liczby 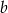 , oraz 70% liczby
, oraz 70% liczby 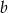 jest równe 60% liczby
jest równe 60% liczby  . Stąd wynika, że iloczyn
. Stąd wynika, że iloczyn 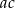 jest równy
jest równy
A) 288 B) 378 C) 324 D) 336
Liczba 81 razy mniejsza od 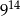 jest równa
jest równa
A) 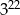 B)
B) 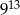 C)
C) 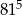 D)
D) 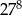
Która z poniższych nierówności jest prawdziwa?
A) 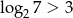 B)
B) 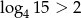 C)
C) 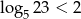 D)
D) 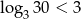
Równość 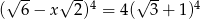 jest
jest
A) prawdziwa dla 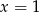 .
.
B) prawdziwa dla 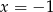 .
.
C) prawdziwa dla 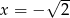 .
.
D) fałszywa dla każdej liczby  .
.
Zbiorem rozwiązań nierówności 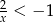 jest zbiór
jest zbiór
A) 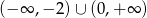 B)
B) 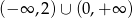 C)
C) 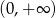 D)
D) 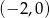
Rozważmy treść następującego zadania:
Obwód rombu o przekątnych długości  i
i 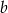 jest równy 48. Pole tego rombu jest równe 16. Oblicz długości przekątnych tego rombu.
jest równy 48. Pole tego rombu jest równe 16. Oblicz długości przekątnych tego rombu.
Który układ równań opisuje zależności między długościami przekątnych tego rombu?
A) 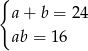 B)
B) 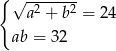 C)
C) 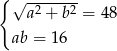 D)
D) 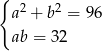
Rysunek przedstawia wykres funkcji 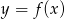 .
.
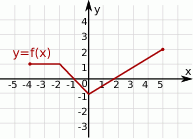
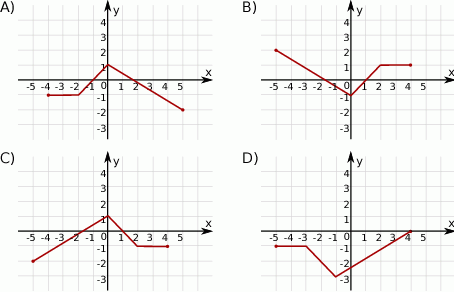
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 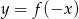 .
.
Miejscem zerowym funkcji liniowej 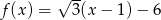 jest liczba
jest liczba
A) 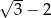 B)
B) 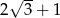 C)
C) 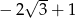 D)
D) 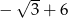
Funkcja kwadratowa 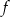 jest określona wzorem
jest określona wzorem 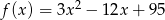 . Zatem wartość
. Zatem wartość 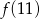 jest równa
jest równa
A) 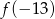 B)
B) 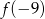 C)
C) 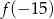 D)
D) 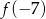
Dwusieczne kątów utworzonych przez przekątne prostokąta 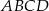 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 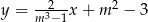 oraz
oraz 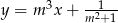 . Zatem
. Zatem
A) 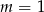 B)
B) 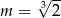 C)
C) 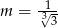 D)
D) 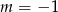
Wskaż wzór funkcji, której wykres ma dokładnie jeden punkt wspólny z prostą 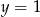 .
.
A) 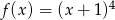 B)
B) 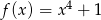 C)
C) 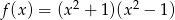 D)
D) 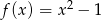
Liczby 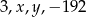 tworzą ciąg geometryczny, wtedy
tworzą ciąg geometryczny, wtedy
A) 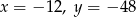 B)
B) 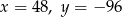 C)
C) 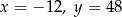 D)
D) 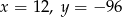
W ciągu arytmetycznym 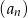 , określonym dla
, określonym dla 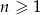 , spełniony jest warunek
, spełniony jest warunek 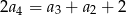 . Różnica
. Różnica  tego ciągu jest równa
tego ciągu jest równa
A) 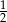 B) 1 C)
B) 1 C) 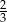 D) 0
D) 0
Kąt  jest ostry i
jest ostry i 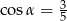 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 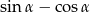 jest równa
jest równa
A) 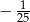 B)
B) 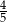 C)
C) 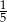 D)
D) 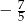
Na okręgu o środku w punkcie 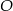 leżą punkty
leżą punkty 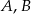 i
i 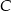 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 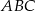 ma miarę
ma miarę 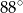 , a kąt
, a kąt 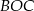 ma miarę o
ma miarę o 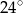 mniejszą od miary kąta
mniejszą od miary kąta 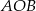 .
.
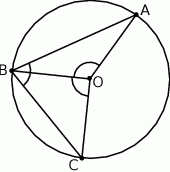
Kąt 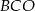 ma miarę
ma miarę
A) 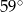 B)
B) 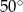 C)
C) 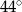 D)
D) 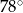
Obwód trójkąta 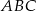 , przedstawionego na rysunku, jest równy
, przedstawionego na rysunku, jest równy
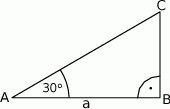
A) 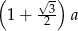 B)
B) 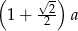 C)
C) 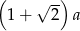 D)
D) 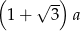
Punkty 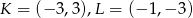 i
i 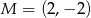 są środkami trzech kolejnych boków rombu. Pole tego rombu jest równe
są środkami trzech kolejnych boków rombu. Pole tego rombu jest równe
A) 80 B) 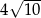 C) 40 D) 20
C) 40 D) 20
Wysokość graniastosłupa prawidłowego czworokątnego, którego pole powierzchni całkowitej jest równe 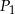 , zwiększono trzykrotnie. Pole powierzchni całkowitej otrzymanego w ten sposób graniastosłupa jest równe
, zwiększono trzykrotnie. Pole powierzchni całkowitej otrzymanego w ten sposób graniastosłupa jest równe 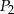 . Zatem
. Zatem
A) 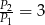 B)
B) 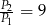 C)
C) 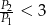 D)
D) 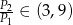
Prosta 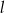 jest nachylona do osi
jest nachylona do osi 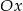 pod kątem
pod kątem 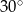 i przecina oś
i przecina oś 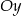 w punkcie
w punkcie 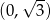 (zobacz rysunek).
(zobacz rysunek).
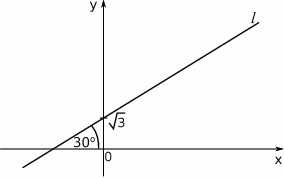
Prosta 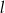 ma równanie
ma równanie
A) 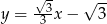 B)
B) 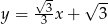 C)
C) 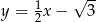 D)
D) 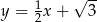
Liczba przekątnych ośmiokąta foremnego jest równa
A) 20 B) 14 C) 21 D) 27
Ile jest wszystkich czterocyfrowych liczb naturalnych większych niż 2018?
A) 7979 B) 7980 C) 7981 D) 7982
Stosunek pola powierzchni bocznej walca do pola przekroju osiowego tego walca
A) może być większy od 6
B) jest zawsze większy od 3
C) może być równy 3
D) jest zawsze mniejszy od 3
Ze zbioru trzydziestu kolejnych liczb naturalnych od 1 do 30 losujemy jedną liczbę. Niech 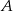 oznacza zdarzenie, że wylosowana liczba będzie dzielnikiem liczby 30. Wtedy prawdopodobieństwo zdarzenia
oznacza zdarzenie, że wylosowana liczba będzie dzielnikiem liczby 30. Wtedy prawdopodobieństwo zdarzenia 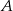 jest równe
jest równe
A) 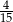 B)
B) 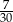 C)
C) 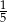 D)
D) 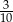
Zadania otwarte
Rozwiąż nierówność 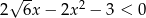 .
.
Dany jest kąt  , dla którego spełniona jest równość
, dla którego spełniona jest równość 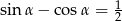 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 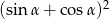 .
.
W ciągu geometrycznym 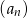 , określonym dla
, określonym dla 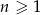 , dane są: wyraz
, dane są: wyraz 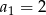 i suma trzech początkowych wyrazów tego ciągu
i suma trzech początkowych wyrazów tego ciągu 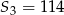 . Wiadomo ponadto, że
. Wiadomo ponadto, że 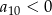 . Oblicz iloraz
. Oblicz iloraz
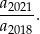
Rozwiąż równanie 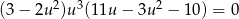 .
.
Dany jest trójkąt prostokątny 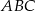 , w którym
, w którym 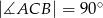 i
i 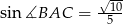 . Niech
. Niech 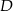 oznacza punkt wspólny wysokości poprowadzonej z wierzchołka
oznacza punkt wspólny wysokości poprowadzonej z wierzchołka 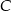 kąta prostego i przeciwprostokątnej
kąta prostego i przeciwprostokątnej 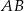 tego trójkąta. Wykaż, że
tego trójkąta. Wykaż, że 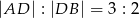 .
.
Dany jest skończony ciąg arytmetyczny o 2018 wyrazach. Wykaż, że średnia arytmetyczna i mediana wszystkich wyrazów tego ciągu są równe.
Parabola, która jest wykresem funkcji kwadratowej 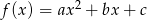 , przechodzi przez punkt
, przechodzi przez punkt 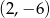 oraz
oraz 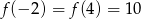 . Oblicz odległość wierzchołka tej paraboli od początku układu współrzędnych.
. Oblicz odległość wierzchołka tej paraboli od początku układu współrzędnych.
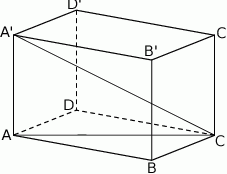
Podstawą graniastosłupa prostego 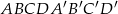 jest romb
jest romb 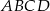 . Przekątna
. Przekątna 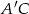 tego graniastosłupa ma długość 6 i jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa ma długość 6 i jest nachylona do płaszczyzny podstawy pod kątem 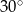 , a objętość graniastosłupa jest równa
, a objętość graniastosłupa jest równa 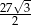 . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa.
Punkt 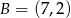 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 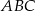 o podstawie
o podstawie 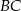 . Pole tego trójkąta jest równe 20, a wysokość poprowadzona z wierzchołka
. Pole tego trójkąta jest równe 20, a wysokość poprowadzona z wierzchołka 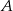 tego trójkąta zawiera się w prostej o równaniu
tego trójkąta zawiera się w prostej o równaniu 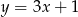 . Oblicz współrzędne punktów
. Oblicz współrzędne punktów 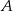 i
i 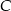 . Rozważ wszystkie przypadki.
. Rozważ wszystkie przypadki.

