/Szkoła średnia/Zadania maturalne/Matura 2018/Matura próbna/CKE, OKE, CEN
Lubelska próba przed maturą
z matematyki (dla klas pierwszych)
poziom rozszerzony 23 maja 2017 Czas pracy: 180 minut
Zadania zamknięte
Wartość wyrażenia 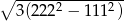 wynosi
wynosi
A) 666 B) 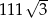 C)
C) 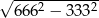 D) 333
D) 333
Wartość wyrażenia 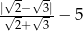 jest równa
jest równa
A) 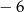 B)
B) 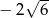 C) 0 D)
C) 0 D) 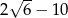
Liczba ![[ ] log4 lo g3(log28 )](https://img.zadania.info/zes/0049446/HzesT7x.gif) jest równa
jest równa
A) 3 B) 0 C) 2 D) 1
Przybliżenie z niedomiarem liczby  jest równe 6, a błąd względny tego przybliżenia wynosi 0,2. Wówczas liczba
jest równe 6, a błąd względny tego przybliżenia wynosi 0,2. Wówczas liczba  jest równa:
jest równa:
A) 4,8 B) 5 C) 7,2 D) 7,5
Liczba 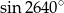 jest równa
jest równa
A) 0 B) 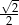 C)
C) 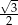 D) 0,5
D) 0,5
Zadania otwarte
Boki trójkąta mają długości: 16, 10, 10. Wyznacz promień okręgu opisanego na tym trójkącie.
Miara  pewnego kąta trójkąta spełnia warunek
pewnego kąta trójkąta spełnia warunek 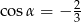 . Wyznacz jego miarę w stopniach. Wynik podaj z dokładnością do 1 stopnia.
. Wyznacz jego miarę w stopniach. Wynik podaj z dokładnością do 1 stopnia.
Po trzykrotnej obniżce ceny towaru za każdym razem o 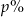 , końcowa cena stanowiła
, końcowa cena stanowiła 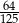 ceny początkowej. Oblicz
ceny początkowej. Oblicz 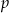 .
.
Uzasadnij, że dla każdej dodatniej liczby całkowitej  liczba
liczba 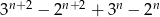 jest wielokrotnością liczby 10.
jest wielokrotnością liczby 10.
Rozwiąż równanie 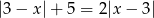 .
.
Podaj współrzędne wszystkich punktów wykresu funkcji określonej wzorem
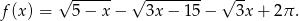
Wykaż, że miara kąta między wysokością trójkąta równoramiennego poprowadzoną do ramienia a podstawą tego trójkąta jest dwa razy mniejsza od miary kąta zawartego między ramionami tego trójkąta.
Każde dwa spośród trzech okręgów są zewnętrznie styczne. Oblicz promienie tych okręgów, jeśli wiadomo, że odległości między ich środkami wynoszą 8, 11, 13.
Zapisz liczbę 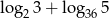 za pomocą
za pomocą  i
i 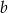 wiedząc, że
wiedząc, że 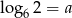 i
i 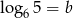 .
.
Suma cyfr liczby dwucyfrowej  jest mniejsza od 12. Różnica tej liczby i liczby dwucyfrowej otrzymanej po przestawieniu jej cyfr jest równa 36. Wyznacz możliwe wartości liczby
jest mniejsza od 12. Różnica tej liczby i liczby dwucyfrowej otrzymanej po przestawieniu jej cyfr jest równa 36. Wyznacz możliwe wartości liczby  .
.
W trójkącie 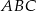 dane są:
dane są: 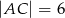 ,
, 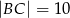 i kąt
i kąt 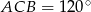 . Wyznacz długość środkowej
. Wyznacz długość środkowej 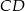 tego trójkąta.
tego trójkąta.
Środkowa 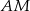 trójkąta
trójkąta 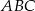 ma długość równą połowie długości boku
ma długość równą połowie długości boku 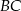 . Miara kąta między tą środkową a wysokością
. Miara kąta między tą środkową a wysokością 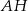 jest równa
jest równa 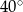 . Wyznacz miary kątów trójkąta
. Wyznacz miary kątów trójkąta 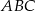 .
.
Oblicz wartość wyrażenia 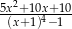 dla
dla 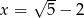 . Wynik zapisz w postaci
. Wynik zapisz w postaci 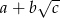 , gdzie
, gdzie 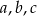 są liczbami naturalnymi.
są liczbami naturalnymi.

