/Szkoła średnia/Zadania maturalne/Matura 2018/Matura próbna/CKE, OKE, CEN
Lubelska próba przed maturą
z matematyki (dla klas pierwszych)
poziom podstawowy grupa I 23 maja 2017 Czas pracy: 170 minut
Zadania zamknięte
Liczba 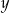 jest o 120% większa od dodatniej liczby
jest o 120% większa od dodatniej liczby  , a liczba
, a liczba  jest pięciokrotnie mniejsza od liczby
jest pięciokrotnie mniejsza od liczby 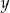 . Zatem
. Zatem
A) 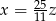 B)
B) 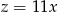 C)
C) 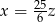 D)
D) 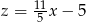
Liczba 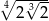 jest równa
jest równa
A) 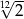 B)
B) 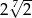 C)
C) 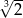 D)
D) 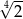
Liczba 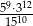 jest równa
jest równa
A) 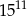 B) 1,8 C)
B) 1,8 C) 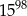 D)
D) 
Liczba 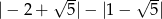 jest równa
jest równa
A) 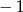 B)
B) 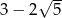 C) 1 D)
C) 1 D) 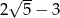
Dane są liczby: 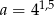 oraz
oraz 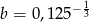 . Zatem
. Zatem
A) 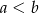 B)
B) 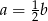 C)
C) 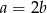 D)
D) 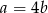
Joanna kupiła 4 batony po 3,20 zł każdy oraz 2,5 kg bananów po 4,20 zł za kilogram. Obliczyła, że za zakupy zapłaci w przybliżeniu 25 zł. Błąd względny tego przybliżenia wynosi:
A) 1,7 B) 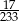 C)
C) 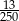 D)
D) 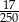
Liczba  jest odwrotnością liczby
jest odwrotnością liczby 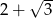 , zaś
, zaś 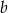 jest liczbą przeciwną do liczby
jest liczbą przeciwną do liczby 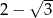 . Różnica
. Różnica 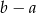 jest wówczas równa:
jest wówczas równa:
A) 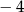 B)
B) 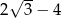 C)
C) 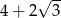 D) 0
D) 0
Liczba 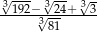 jest równa
jest równa
A) 1 B) 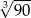 C)
C) 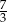 D)
D) 
Wyrażenie 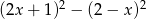 jest równe wyrażeniu
jest równe wyrażeniu
A) 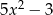 B)
B) 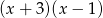 C)
C) 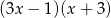 D)
D) 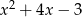
Dany jest zbiór 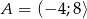 . Do zbioru
. Do zbioru 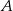 należy
należy
A) 12 liczb całkowitych i 5 liczb pierwszych
B) 13 liczb całkowitych i 9 liczb naturalnych
C) 6 liczb naturalnych i 4 liczby pierwsze
D) 12 liczb całkowitych i 4 liczby pierwsze
Dane jest równanie 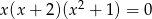 . Do zbioru rozwiązań tego równania należy liczba
. Do zbioru rozwiązań tego równania należy liczba
A) 2 B) 1 C) 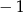 D) 0
D) 0
Najmniejszą liczbą całkowitą, która nie spełnia nierówności 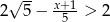 jest
jest
A) 11 B) 14 C) 12 D) 22
Układ równań 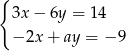 opisuje w układzie współrzędnych zbiór pusty dla
opisuje w układzie współrzędnych zbiór pusty dla
A) 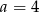 B)
B) 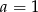 C)
C) 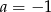 D)
D) 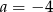
Jedno z ramion kąta  (rysunek) leży na osi odciętych, a drugie przechodzi przez punkt
(rysunek) leży na osi odciętych, a drugie przechodzi przez punkt 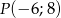 .
.
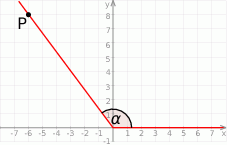
Zatem 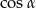 jest równy
jest równy
A) 0,8 B) 0,6 C) 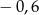 D)
D) 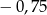
Wartość wyrażenia 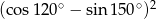 jest równa
jest równa
A) 1 B) 0 C) 3 D) 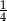
Jedna z przyprostokątnych trójkąta prostokątnego ma długość 15 cm, a przeciwprostokątna 17 cm. Tangens najmniejszego kąta w tym trójkącie jest równy:
A) 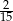 B)
B) 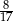 C)
C) 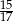 D)
D) 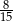
Niech  i
i 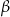 oznaczają miary kątów ostrych w dowolnym trójkącie prostokątnym. Wówczas zachodzi równość:
oznaczają miary kątów ostrych w dowolnym trójkącie prostokątnym. Wówczas zachodzi równość:
A) 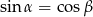 B)
B) 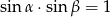 C)
C) 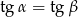 D)
D) 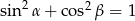
Długość boku trójkąta równobocznego wynosi 12. Pole koła wpisanego w ten trójkąt jest równe
A) 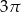 B)
B) 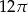 C)
C) 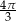 D)
D) 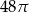
Na poniższym rysunku punkt 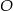 jest środkiem okręgu.
jest środkiem okręgu.
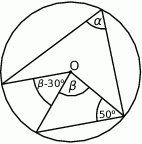
Miara kąta  jest równa
jest równa
A) 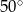 B)
B) 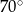 C)
C) 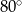 D)
D) 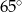
Obwód trójkąta 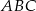 jest równy 40 cm. Punkt
jest równy 40 cm. Punkt 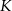 leży na boku
leży na boku 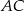 , a punkt
, a punkt 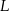 na boku
na boku 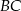 tak, że odcinek
tak, że odcinek 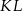 jest równoległy do boku
jest równoległy do boku 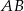 trójkąta i
trójkąta i 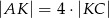 . Obwód trójkąta
. Obwód trójkąta 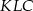 jest równy:
jest równy:
A) 10 cm B) 4 cm C) 8 cm D) 5 cm
Ramię trójkąta równoramiennego ma długość 12 i tworzy z podstawą kąt o mierze 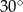 . Obwód tego trójkąta jest równy:
. Obwód tego trójkąta jest równy:
A) 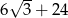 B) 30 C) 36 D)
B) 30 C) 36 D) 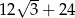
Dziedziną funkcji 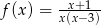 jest zbiór:
jest zbiór:
A) 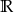 B)
B) 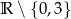 C)
C) 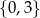 D)
D) 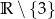
Funkcja 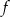 jest określona wzorem
jest określona wzorem 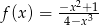 . Wartość tej funkcji dla argumentu równego
. Wartość tej funkcji dla argumentu równego 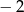 wynosi:
wynosi:
A) 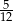 B)
B) 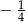 C)
C)  D)
D) 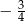
Funkcja 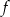 określona jest wzorem
określona jest wzorem 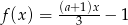 . Liczba
. Liczba 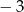 jest miejscem zerowym tej funkcji dla
jest miejscem zerowym tej funkcji dla  równego:
równego:
A) 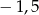 B)
B) 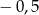 C)
C) 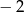 D)
D) 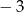
Dziedziną funkcji 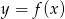 jest przedział
jest przedział 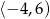 . Zatem dziedziną funkcji
. Zatem dziedziną funkcji 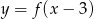 jest zbiór
jest zbiór
A) 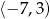 B)
B) 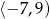 C)
C) 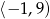 D)
D) 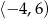
Zadania otwarte
Rozwiąż nierówność 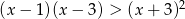 .
.
Wykaż, że liczba 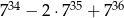 jest podzielna przez 12.
jest podzielna przez 12.
Wiedząc, że 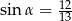 i
i 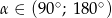 , oblicz
, oblicz 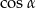 oraz
oraz 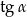 .
.
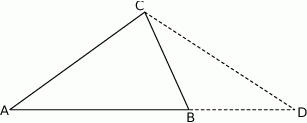
W trójkącie 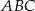 przedłużono bok
przedłużono bok 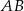 poza wierzchołek
poza wierzchołek 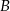 i odłożono odcinek
i odłożono odcinek 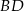 taki, że
taki, że 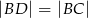 . Następnie połączono punkty
. Następnie połączono punkty 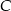 i
i 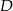 (rysunek). Wykaż, że
(rysunek). Wykaż, że 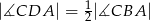 .
.
Jeden z kątów trójkąta jest cztery razy większy od drugiego oraz o 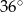 mniejszy od trzeciego kąta. Oblicz miary wszystkich kątów tego trójkąta.
mniejszy od trzeciego kąta. Oblicz miary wszystkich kątów tego trójkąta.
W wyborach do samorządu szkolnego uczniowie oddawali głos na jednego z trzech kandydatów: Adama, Olę albo Kasię. Wszystkie oddane głosy były ważne. Adam uzyskał 20% wszystkich głosów, a Ola 65%. Kasia otrzymała 72 głosy.
- Ilu uczniów brało udział w głosowaniu?
- O ile procent więcej głosów otrzymała Ola niż Adam?
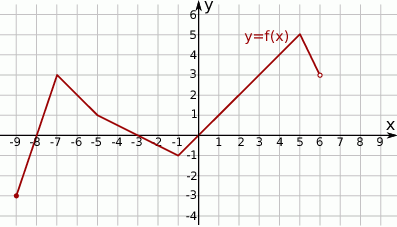
Poniżej przedstawiony jest wykres funkcji 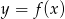 . Na podstawie tego wykresu podaj:
. Na podstawie tego wykresu podaj:
- dziedzinę i zbiór wartości funkcji
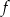 ,
, - maksymalne przedziały, w których funkcja jest malejąca,
- zbiór argumentów, dla których funkcja przyjmuje wartości nieujemne,
- zbiór rozwiązań nierówności
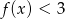 .
. - Naszkicuj (na tym samym rysunku) wykres funkcji
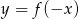 .
.
Pan Michał jechał z miejscowości 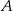 do miejscowości
do miejscowości 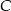 przez miejscowość
przez miejscowość 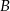 . Droga z
. Droga z 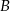 do
do 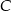 jest o 60 km dłuższa niż droga z
jest o 60 km dłuższa niż droga z 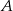 do
do 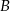 . Trasę pomiędzy miejscowościami
. Trasę pomiędzy miejscowościami 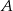 i
i 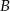 pan Michał pokonał ze średnią prędkością 70 km/h. Z miejscowości
pan Michał pokonał ze średnią prędkością 70 km/h. Z miejscowości 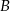 do
do 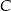 jechał średnio 90 km/h. Średnia prędkość całego przejazdu wyniosła 80 km/h. Jaką drogę przejechał pan Michał z
jechał średnio 90 km/h. Średnia prędkość całego przejazdu wyniosła 80 km/h. Jaką drogę przejechał pan Michał z 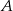 do
do 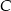 ?
?
W trójkącie prostokątnym jedna z przyprostokątnych ma długość 15 cm, a przeciwprostokątna jest o 9 cm dłuższa od drugiej przyprostokątnej. Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego.

