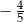Zadanie nr 4010007
Oblicz wartość wyrażenia 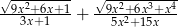 dla
dla 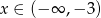 .
.
Rozwiązanie
Zauważmy, że pod każdym z pierwiastków mamy pełen kwadrat.
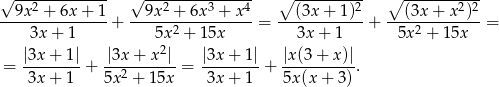
Zauważmy teraz, że z założenia 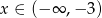 mamy
mamy 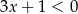 i
i 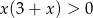 , więc
, więc
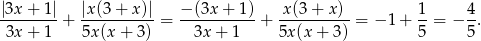
Odpowiedź: 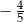
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz wartość wyrażenia 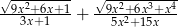 dla
dla 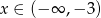 .
.
Zauważmy, że pod każdym z pierwiastków mamy pełen kwadrat.
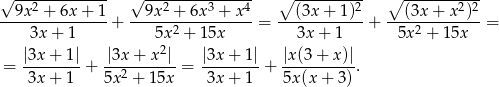
Zauważmy teraz, że z założenia 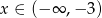 mamy
mamy 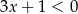 i
i 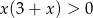 , więc
, więc
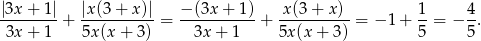
Odpowiedź: