/Szkoła średnia/Liczby/Wyrażenia algebraiczne/Oblicz wartość wyrażenia/2 literki

Zadanie nr 4266556

Dodaj do ulubionych
Dodaj do rozwiązanych

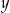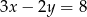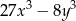Między liczbami rzeczywistymi x i y zachodzi związek 3x − 2y = 8 . Wyznacz najmniejszą wartość wyrażenia 27x3 − 8y3 .

Rozwiązanie

Sposób I

Korzystamy ze wzoru skróconego mnożenia na różnicę sześcianów, a następnie ze wzoru kwadrat różnicy

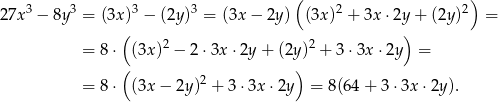
3 3 3 3 ( 2 2) 27x − 8y = (3x) − (2y) = (3x − 2y ) (3x) + 3x⋅ 2y+ (2y) = ( 2 2 ) = 8⋅ (3x) − 2 ⋅3x ⋅2y + (2y) + 3 ⋅3x ⋅2y = ( ) = 8⋅ (3x − 2y)2 + 3 ⋅3x ⋅2y = 8(64 + 3 ⋅3x ⋅2y).

Podstawiamy teraz w tym wyrażeniu 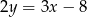2y = 3x − 8 .

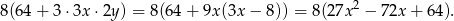
8(64 + 3 ⋅3x ⋅2y) = 8 (6 4+ 9x(3x − 8)) = 8 (27x2 − 72x + 64).

Wykresem trójmianu w nawiasie jest parabola o ramionach skierowanych w górę, więc najmniejszą wartość przyjmuje on w wierzchołku, czyli dla 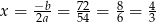x = −2ba-= 7524 = 86 = 43 . Wartość ta jest równa

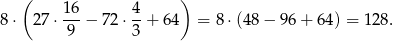
( ) 8 ⋅ 27⋅ 16-− 72 ⋅ 4-+ 64 = 8⋅(48 − 96 + 6 4) = 128. 9 3

Sposób II

Zauważmy najpierw, że

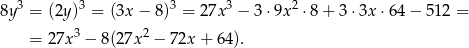
8y3 = (2y )3 = (3x − 8)3 = 27x 3 − 3⋅9x 2 ⋅8 + 3 ⋅3x ⋅64 − 512 = 3 2 = 2 7x − 8(27x − 72x + 6 4).

Mamy zatem

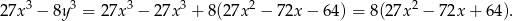
27x3 − 8y 3 = 27x3 − 27x3 + 8(2 7x2 − 72x − 64) = 8 (27x2 − 72x + 64 ).

Najmniejszą wartość tego wyrażenia wyznaczamy tak samo jak w poprzednim sposobie.  
Odpowiedź: 128

Wersja PDF