Zadanie nr 3866878
Wiadomo, że 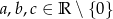 oraz
oraz 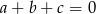 . Oblicz wartość sumy
. Oblicz wartość sumy
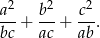
Rozwiązanie
Sposób I
Przekształcamy interesujące nas wyrażenie korzystając ze wzoru na sumę sześcianów oraz danej równości 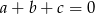 .
.
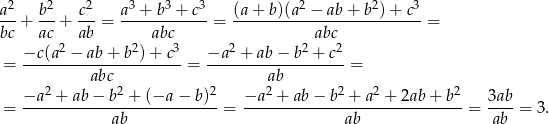
Sposób II
Podstawiamy 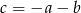 w danym wyrażeniu.
w danym wyrażeniu.
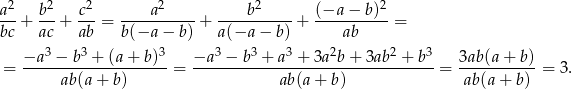
Odpowiedź: 3
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wiadomo, że 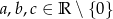 oraz
oraz 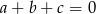 . Oblicz wartość sumy
. Oblicz wartość sumy
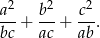
Sposób I
Przekształcamy interesujące nas wyrażenie korzystając ze wzoru na sumę sześcianów oraz danej równości 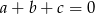 .
.
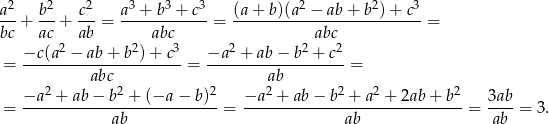
Sposób II
Podstawiamy 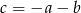 w danym wyrażeniu.
w danym wyrażeniu.
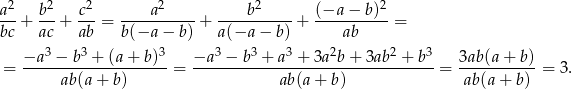
Odpowiedź: 3
