/Gimnazjum/Egzamin gimnazjalny/Egzamin 2018
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 14 kwietnia 2018 Czas pracy: 90 minut
Informacja do zadań 1 i 2
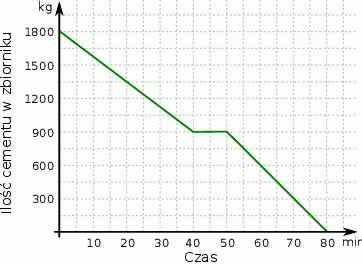
Zbiornik z cementem jest opróżniany na znajdujący się pod nim taśmociąg. Na wykresie przedstawiono ilość cementu pozostałego w zbiorniku w zależności od czasu upływającego od momentu rozpoczęcia opróżniania zbiornika.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Średnia prędkość z jaką opróżniono pierwszą połowę zawartości zbiornika wyniosła
A) 1350 kg/h B) 800 kg/h C) 2250 kg/h D) 1080 kg/h
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Na 10 minut przed zakończeniem opróżniania zbiornika wciąż było w nim 300 kg cementu. | P | F |
| W trakcie pierwszych dwudziestu minut opróżniania zbiornika wysypano z niego 1350 kg cementu. | P | F |
Sonda Voyager 2, która została wysłana w przestrzeń kosmiczną w 1977 roku, w 2007 roku znalazła się na granicy heliosfery w odległości 17,5 bilionów kilometrów od słońca. Od tej pory sonda oddala się od słońca ze stałą prędkością równą 15,35 km/s.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Prędkość sondy Voyager 2 po opuszczeniu heliosfery jest równa
A) 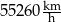 B)
B) 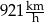 C)
C) 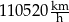 D)
D) 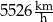
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Zaokrąglenie ułamka okresowego 3,5(4) z dokładnością do 0,001 jest równe
A) 3,543 B) 3,545 C) 3,544 D) 3,546
Na planie wykonanym w skali 1 : 300 prostokątna podłoga ma pole 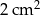 .
.
Dokończ zdanie. Zaznacz dobrą odpowiedź.
Pole powierzchni tej podłogi jest równe
A) 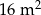 B)
B) 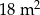 C)
C) 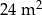 D)
D) 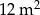
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 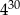 jest 128 razy większa od liczby jest 128 razy większa od liczby 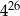 . . | P | F |
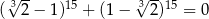 | P | F |
Która równość jest fałszywa? Wybierz odpowiedź spośród podanych.
A) 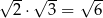 B)
B) 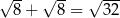 C)
C) 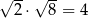 D)
D) 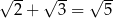
W pewnej szkole do egzaminu gimnazjalnego przystąpiło o 20 chłopców mniej niż dziewcząt. Chłopcy stanowili 45% liczby osób piszących egzamin. Ile dziewcząt przystąpiło do tego egzaminu? Wybierz właściwą odpowiedź spośród podanych.
A) 140 B) 110 C) 120 D) 90
Na osi liczbowej dane są liczby  i
i 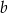
![]()
Liczby  i
i 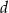 są zaokrągleniami odpowiednio liczb
są zaokrągleniami odpowiednio liczb  i
i 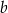 do części setnych. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
do części setnych. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Suma  jest równa:
jest równa:
A) 0,22 B) 0,14 C) 0,07 D) 0,08
Na rysunku przedstawiono sposób ułożenia wzoru z jednakowych równoległoboków i trapezów równoramiennych oraz podano długości trzech fragmentów tego wzoru.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Fragment wzoru oznaczony na rysunku znakiem zapytania ma długość
A) 42 cm B) 36 cm C) 54 cm D) 38 cm
Cztery kartoniki z cyframi 0, 0, 1, 4 układamy tak, aby otrzymać liczbę czterocyfrową.
![]()
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jest 12 liczb czterocyfrowych, które możemy utworzyć w ten sposób. | P | F |
Prawdopodobieństwo, że utworzona w ten sposób liczba czterocyfrowa dzieli się przez 4 jest równe 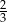 . . | P | F |
Uczniowie mieli wyznaczyć zmienną 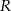 ze wzoru
ze wzoru 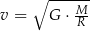 . W tabeli przedstawiono rezultaty pracy kilkorga z nich.
. W tabeli przedstawiono rezultaty pracy kilkorga z nich.
| Uczeń | Beata | Kacper | Wojtek | Ania |
| Rezultat | 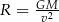 | 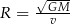 | 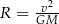 | 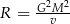 |
Kto z uczniów poprawnie wyznaczył zmienną  ? Wybierz właściwą odpowiedź spośród podanych.
? Wybierz właściwą odpowiedź spośród podanych.
A) Beata B) Kacper C) Wojtek D) Ania
Funkcja 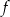 przyporządkowuje każdej liczbie naturalnej większej od 1 sumę jej cyfr.
przyporządkowuje każdej liczbie naturalnej większej od 1 sumę jej cyfr.
Liczba  dla której prawdziwa jest równość
dla której prawdziwa jest równość
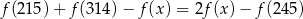
może być równa
A) 2114 B) 3115 C) 1611 D) 4103
W sześciokącie 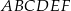 poprowadzono trzy przekątne wychodzące z wierzchołka
poprowadzono trzy przekątne wychodzące z wierzchołka 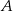 i utworzone przez nie kąty spełniają warunki:
i utworzone przez nie kąty spełniają warunki: 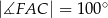 ,
, 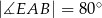 ,
, 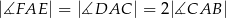 .
.
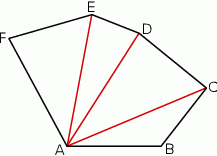
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
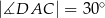 | P | F |
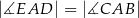 | P | F |
Na którym z rysunków zaznaczony kąt  nie ma miary
nie ma miary 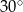 .
.
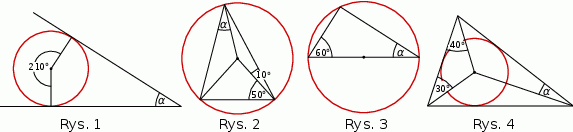
Wybierz właściwą odpowiedź spośród podanych.
A) na rysunku 1 B) na rysunku 2 C) na rysunku 3 D) na rysunku 4
Wysokości 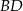 i
i 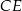 trójkąta równobocznego
trójkąta równobocznego 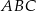 przecinają się w punkcie
przecinają się w punkcie 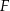 .
.
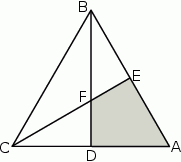
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole czworokąta 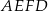 stanowi stanowi 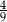 pola trójkąta pola trójkąta 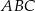 . . | P | F |
Jeden z kątów czworokąta 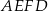 ma miarę ma miarę 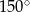 . . | P | F |
Promienie okręgów o środkach 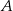 i
i 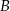 są odpowiednio równe 2018 i 995. Długość odcinka
są odpowiednio równe 2018 i 995. Długość odcinka 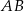 jest równa 1020.
jest równa 1020.
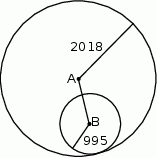
Czy okręgi te mają punkt wspólny? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | długość odcinka 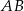 jest mniejsza od 1023. jest mniejsza od 1023. |
| B) | okręgi są styczne wewnętrznie. |
| C) | długość odcinka 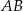 jest mniejsza od promienia większego okręgu. jest mniejsza od promienia większego okręgu. |
Prostopadłościan o wymiarach 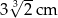 ,
, 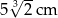 i
i 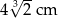 podzielono na 60 jednakowych sześcianów.
podzielono na 60 jednakowych sześcianów.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Objętość jednego sześcianu jest równa
A) 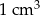 B)
B) 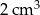 C)
C) 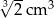 D)
D) 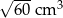
Rysunek przedstawia siatkę ostrosłupa prostego o podstawie będącej prostokątem.
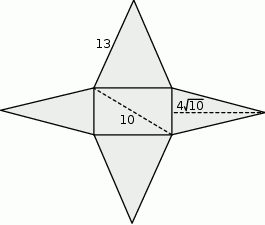
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Objętość tego ostrosłupa jest równa
A) 192 B) 96 C) 576 D) 384
Dagmara z 20 jednakowych sześciennych kostek skleiła figurę, której widok z przodu i z tyłu przedstawiono na rysunkach.

Całą figurę, również od spodu, Dagmara pomalowała. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Dokładnie 7 kostek ma pomalowane dokładnie 3 ściany. | P | F |
| Dokładnie 7 kostek ma pomalowane dokładnie 2 ściany. | P | F |
Jeżeli na końcu liczby trzycyfrowej dopiszemy 23, to liczba ta zwiększy się o 43286. Jaka liczba trzycyfrowa ma tę własność?
Na rysunku przedstawiono plany trzech działek. Pole powierzchni każdej z nich jest takie samo. Oblicz sumę obwodów tych trzech działek.

Dwa pojemniki mają kształt graniastosłupów prawidłowych, przy czym pierwszy ma kształt graniastosłupa trójkątnego o krawędzi podstawy długości 30 cm, a drugi sześciokątnego o wysokości 50 cm. Objętość pierwszego pojemnika stanowi 45% objętości drugiego pojemnika i jest mniejsza od tej objętości o 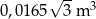 . Oblicz objętości obu pojemników. Zapisz obliczenia.
. Oblicz objętości obu pojemników. Zapisz obliczenia.