/Szkoła średnia/Zadania maturalne/Matura 2018/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 17 marca 2018 Czas pracy: 170 minut
Zadania zamknięte
Liczba 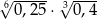 jest równa
jest równa
A) 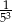 B) 125 C) 0,04 D)
B) 125 C) 0,04 D) 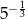
Iloczyn dodatnich liczb  i
i 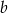 jest równy 700. Ponadto 70% liczby
jest równy 700. Ponadto 70% liczby  jest równe 40% liczby
jest równe 40% liczby 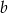 . Stąd wynika, że
. Stąd wynika, że 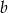 jest równe
jest równe
A) 49 B) 35 C) 45 D) 50
Liczba 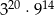 jest równa
jest równa
A) 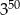 B)
B) 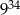 C)
C) 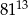 D)
D) 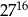
Punkt 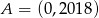 należy do wykresu funkcji
należy do wykresu funkcji 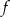 określonej wzorem
określonej wzorem
A) 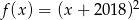
B) 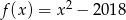
C) 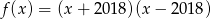
D) 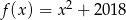
Równość 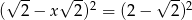 jest
jest
A) prawdziwa dla 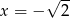 .
.
B) prawdziwa dla 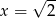 .
.
C) prawdziwa dla 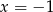 .
.
D) fałszywa dla każdej liczby  .
.
Rozwiązaniami równania 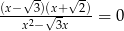 jest
jest
A) tylko 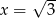 B)
B) 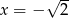 i
i 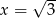 C) tylko
C) tylko 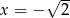 D)
D) 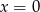 i
i 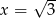
Liczba 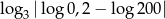 jest równa liczbie
jest równa liczbie
A) 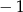 B) 0 C) 1 D) 3
B) 0 C) 1 D) 3
Rozważmy treść następującego zadania:
Pole prostokąta o bokach długości  i
i 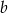 jest równe 40. Jeden z boków tego prostokąta jest o 15 krótszy od drugiego. Oblicz długości boków tego prostokąta.
jest równe 40. Jeden z boków tego prostokąta jest o 15 krótszy od drugiego. Oblicz długości boków tego prostokąta.
Który układ równań opisuje zależności między długościami boków tego prostokąta?
A) 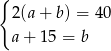 B)
B) 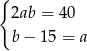 C)
C) 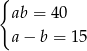 D)
D) 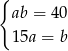
Jednym z miejsc zerowych funkcji kwadratowej 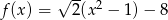 jest liczba
jest liczba
A) 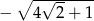 B)
B) 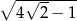 C)
C) 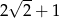 D)
D) 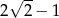
Funkcja kwadratowa 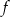 jest określona wzorem
jest określona wzorem 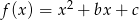 oraz
oraz 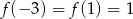 . Współczynnik
. Współczynnik 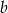 jest równy
jest równy
A) 0 B) 1 C) 2 D) 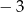
Gdy przesuniemy wykres funkcji 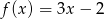 o 3 jednostki w lewo i 2 jednostki w dół, to otrzymamy wykres funkcji opisanej wzorem
o 3 jednostki w lewo i 2 jednostki w dół, to otrzymamy wykres funkcji opisanej wzorem
A) 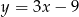 B)
B) 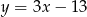 C)
C) 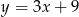 D)
D) 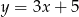
Na płaszczyźnie z układem współrzędnych proste 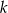 i
i 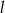 przecinają się pod kątem prostym w punkcie
przecinają się pod kątem prostym w punkcie 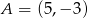 . Prosta
. Prosta 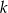 jest określona równaniem
jest określona równaniem 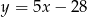 . Zatem prostą
. Zatem prostą 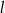 opisuje równanie
opisuje równanie
A) 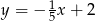 B)
B) 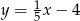 C)
C) 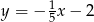 D)
D) 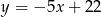
Dany jest czterowyrazowy ciąg arytmetyczny 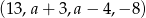 . Wynika stąd, że
. Wynika stąd, że
A) 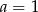 B)
B) 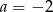 C)
C) 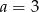 D)
D) 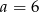
W rosnącym ciągu geometrycznym 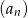 , określonym dla
, określonym dla 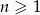 , spełniony jest warunek
, spełniony jest warunek 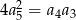 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 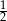 B)
B) 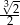 C)
C) 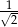 D)
D) 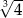
Kąt  jest rozwarty i spełniona jest równość
jest rozwarty i spełniona jest równość 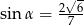 . Stąd wynika, że
. Stąd wynika, że
A) 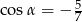 B)
B) 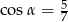 C)
C) 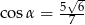 D)
D) 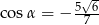
W trójkącie 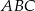 punkt
punkt 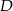 leży na boku
leży na boku 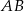 , punkt
, punkt 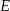 leży na boku
leży na boku 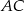 , a ponadto odcinek
, a ponadto odcinek 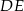 jest równoległy do boku
jest równoległy do boku 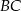 i
i 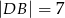 . Pole trójkąta
. Pole trójkąta 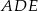 jest równe 12, a pole trapezu
jest równe 12, a pole trapezu 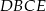 jest równe 15 (zobacz rysunek).
jest równe 15 (zobacz rysunek).
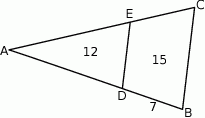
Odcinek 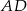 ma długość
ma długość
A) 5,6 B) 12 C) 14 D) 9
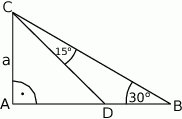
Obwód trójkąta 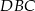 , przedstawionego na rysunku, jest równy
, przedstawionego na rysunku, jest równy
A) 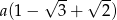 B)
B) 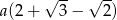 C)
C) 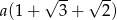 D)
D) 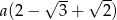
Punkty 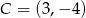 i
i 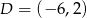 są dwoma sąsiednimi wierzchołkami kwadratu
są dwoma sąsiednimi wierzchołkami kwadratu 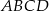 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 117 B) 85 C) 13 D) 45
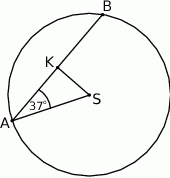
W okręgu o środku w punkcie 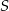 poprowadzono cięciwę
poprowadzono cięciwę 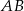 , która utworzyła z promieniem
, która utworzyła z promieniem 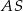 kąt o mierze
kąt o mierze 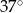 (zobacz rysunek). Promień tego okręgu ma długość 10. Długość cięciwy
(zobacz rysunek). Promień tego okręgu ma długość 10. Długość cięciwy 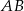 jest liczbą z przedziału
jest liczbą z przedziału
A) 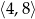 B)
B) 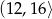 C)
C) 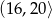 D)
D) 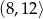
Ile jest wszystkich liczb pięciocyfrowych, większych 53079, utworzonych wyłącznie z cyfr 2, 3, 4, 5 przy założeniu, że cyfry mogą się powtarzać, ale nie wszystkie z tych cyfr muszą być wykorzystane?
A) 48 B) 15 C) 128 D) 192
Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego, w którym wysokość jest 3 razy krótsza od krawędzi podstawy, jest równe 60. Zatem krawędź podstawy tego graniastosłupa jest równa
A) 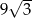 B)
B) 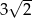 C)
C) 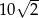 D)
D) 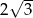
Pole powierzchni bocznej walca jest równe 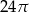 , a promień jego podstawy ma długość 4. Wysokość tego walca jest równa
, a promień jego podstawy ma długość 4. Wysokość tego walca jest równa
A) 6 B) 3 C) 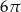 D)
D) 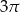
Prosta 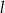 tworzy z osią
tworzy z osią 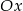 kąt
kąt 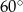 i przecina oś
i przecina oś 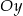 w punkcie
w punkcie 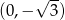 (zobacz rysunek).
(zobacz rysunek).
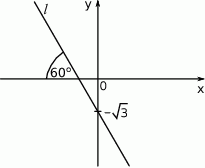
Prosta 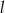 ma równanie
ma równanie
A) 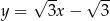 B)
B) 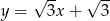 C)
C) 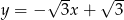 D)
D) 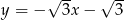
Punkt O jest środkiem okręgu (rysunek).
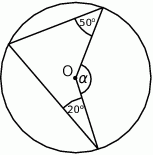
Miara kąta  jest równa
jest równa
A) 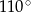 B)
B) 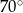 C)
C) 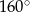 D)
D) 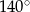
Ze zbioru pięćdziesięciu kolejnych liczb naturalnych od 1 do 50 losujemy dwie liczby  i
i 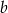 takie, że
takie, że 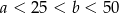 . Prawdopodobieństwo, że liczba
. Prawdopodobieństwo, że liczba 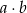 jest podzielna przez 50 jest równe
jest podzielna przez 50 jest równe
A) 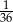 B)
B) 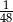 C)
C) 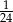 D)
D) 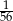
Zadania otwarte
Rozwiąż nierówność 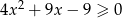 .
.
Kąt  jest ostry oraz
jest ostry oraz 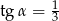 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 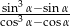 .
.
W ciągu arytmetycznym 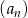 , określonym dla
, określonym dla 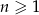 , dane są: wyraz
, dane są: wyraz 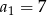 i suma czterech początkowych wyrazów tego ciągu
i suma czterech początkowych wyrazów tego ciągu 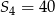 . Oblicz różnicę
. Oblicz różnicę 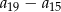 .
.
Rozwiąż równanie 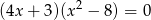 .
.
W trójkącie prostokątnym jedna przyprostokątna jest 3 razy dłuższa od drugiej. Wykaż, że wysokość opuszczona na przeciwprostokątną dzieli ją na odcinki, z których jeden jest 9 razy dłuższy od drugiego.
Wykaż, że dla dowolnych liczb rzeczywistych 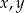 prawdziwa jest nierówność
prawdziwa jest nierówność
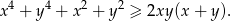
Funkcja kwadratowa 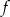 jest określona dla wszystkich liczb rzeczywistych
jest określona dla wszystkich liczb rzeczywistych  wzorem
wzorem 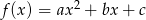 . Najmniejsza wartość funkcji
. Najmniejsza wartość funkcji 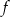 jest równa
jest równa 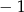 oraz
oraz 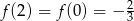 . Oblicz wartość współczynnika
. Oblicz wartość współczynnika  .
.
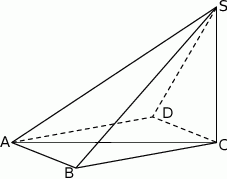
Podstawą ostrosłupa 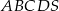 jest romb
jest romb 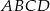 . Krawędź
. Krawędź 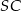 jest prostopadła do płaszczyzny podstawy, krawędź
jest prostopadła do płaszczyzny podstawy, krawędź 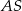 ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem
ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 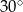 . Krawędź
. Krawędź 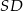 ma długość
ma długość 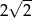 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Dane są punkty 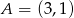 i
i 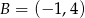 oraz prosta
oraz prosta 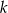 o równaniu
o równaniu 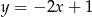 . Wyznacz taki punkt
. Wyznacz taki punkt 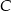 prostej
prostej 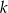 , aby suma kwadratów boków trójkąta
, aby suma kwadratów boków trójkąta 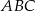 była najmniejsza możliwa. Oblicz tę najmniejszą sumę kwadratów długości boków.
była najmniejsza możliwa. Oblicz tę najmniejszą sumę kwadratów długości boków.

