/Szkoła średnia/Zadania maturalne/Matura 2018/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 24 marca 2018 Czas pracy: 180 minut
Zadania zamknięte
Liczba 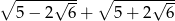 jest równa
jest równa
A) 12 B) 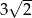 C) 4 D)
C) 4 D) 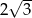
Granica 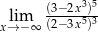 jest równa
jest równa
A) 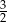 B)
B) 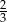 C)
C) 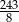 D)
D) 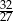
Punkt 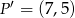 jest obrazem punktu
jest obrazem punktu 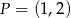 w jednokładności o środku w punkcie
w jednokładności o środku w punkcie 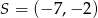 . Skala tej jednokładności jest równa
. Skala tej jednokładności jest równa
A)  B)
B) 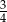 C) 3 D)
C) 3 D) 
Na rysunku przedstawiono fragment wykresu pochodnej 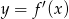 funkcji
funkcji 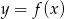 .
.
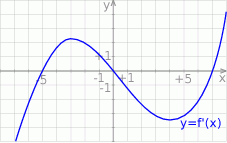
Wynika stąd, że funkcja 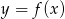 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 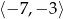 B)
B) 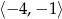 C)
C) 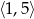 D)
D) 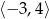
Liczba 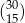 jest podzielna przez
jest podzielna przez
A) 7 B) 55 C) 143 D) 85
Zadania otwarte
Wykaż, że jeżeli 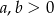 i
i 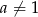 , to dla dowolnej liczby całkowitej dodatniej
, to dla dowolnej liczby całkowitej dodatniej  prawdziwy jest wzór
prawdziwy jest wzór
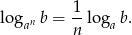
Reszta z dzielenia wielomianu 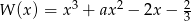 przez dwumian
przez dwumian 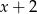 jest równa 1. Oblicz wartość współczynnika
jest równa 1. Oblicz wartość współczynnika  .
.
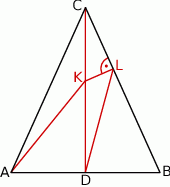
Odcinek 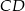 jest wysokością przedstawionego na rysunku trójkąta równoramiennego
jest wysokością przedstawionego na rysunku trójkąta równoramiennego 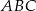 , w którym
, w którym 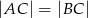 . Punkt
. Punkt 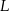 jest rzutem punktu
jest rzutem punktu 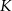 wysokości
wysokości 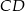 na bok
na bok 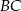 . Udowodnij, że
. Udowodnij, że 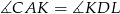 .
.
Na stu mężczyzn ośmiu, zaś na tysiąc kobiet pięć ma zaburzenie rozpoznawania barw. Z grupy, w której stosunek liczby mężczyzn do liczby kobiet wynosi 7:11 wybrano losowo jedną osobę. Jakie jest prawdopodobieństwo, że wylosowana osoba prawidłowo rozpoznaje kolory?
Na bokach 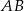 i
i 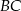 trójkąta
trójkąta 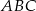 wybrano punkty
wybrano punkty 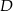 i
i 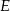 w ten sposób, że odcinek
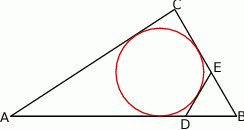
w ten sposób, że odcinek 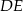 jest styczny do okręgu wpisanego w trójkąt
jest styczny do okręgu wpisanego w trójkąt 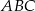 oraz trójkąt
oraz trójkąt 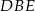 jest równoboczny. Obwód trójkąta
jest równoboczny. Obwód trójkąta 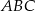 jest równy 20, a długość boku
jest równy 20, a długość boku 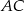 jest równa 7. Oblicz pole trójkąta
jest równa 7. Oblicz pole trójkąta 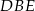 .
.
Funkcja 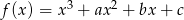 ma trzy różne miejsca zerowe:
ma trzy różne miejsca zerowe: 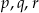 . Wykaż, że
. Wykaż, że
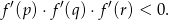
Oblicz pole trójkąta ograniczonego osią 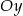 oraz stycznymi do wykresu funkcji
oraz stycznymi do wykresu funkcji 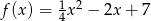 poprowadzonymi w punktach
poprowadzonymi w punktach 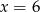 i
i 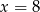 .
.
Rozwiąż równanie 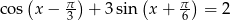 w przedziale
w przedziale 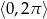 .
.
Tworzącą stożka widać ze środka kuli wpisanej w ten stożek pod kątem o mierze  . Wyznacz stosunek objętości tej kuli do objętości stożka.
. Wyznacz stosunek objętości tej kuli do objętości stożka.
Funkcje 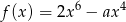 ,
, 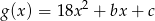 i
i 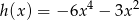 mają tę własność, że dla każdej liczby rzeczywistej
mają tę własność, że dla każdej liczby rzeczywistej 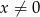 , liczby
, liczby 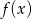 ,
, 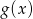 i
i 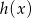 tworzą (w pewnej ustalonej kolejności) ciąg geometryczny. Wykaż, że funkcja
tworzą (w pewnej ustalonej kolejności) ciąg geometryczny. Wykaż, że funkcja 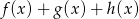 jest rosnąca na przedziale
jest rosnąca na przedziale 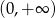 .
.
Napisz równanie okręgu opisanego na trapezie równoramiennym 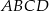 , jeżeli
, jeżeli 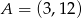 ,
, 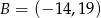 ,
, 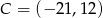 i
i 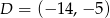 .
.
W ostrosłup prawidłowy czworokątny o wysokości 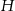 wpisano sześcian tak, że cztery jego wierzchołki należą do krawędzi bocznych ostrosłupa, a cztery pozostałe należą do płaszczyzny jego podstawy. Oblicz dla jakiej długości krawędzi podstawy ostrosłupa stosunek objętości ostrosłupa do objętości sześcianu jest najmniejszy możliwy.
wpisano sześcian tak, że cztery jego wierzchołki należą do krawędzi bocznych ostrosłupa, a cztery pozostałe należą do płaszczyzny jego podstawy. Oblicz dla jakiej długości krawędzi podstawy ostrosłupa stosunek objętości ostrosłupa do objętości sześcianu jest najmniejszy możliwy.

