/Szkoła średnia/Zadania maturalne/Matura 2018/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 7 kwietnia 2018 Czas pracy: 170 minut
Zadania zamknięte
Wyrażenie 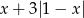 dla
dla 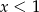 ma wartość
ma wartość
A) 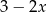 B)
B) 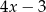 C)
C)  D) 3
D) 3
Wartość liczbowa wyrażenia 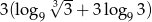 jest równa
jest równa
A) 3,5 B) 9 C) 5 D) 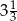
Suma 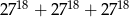 jest równa
jest równa
A) 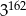 B)
B) 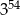 C)
C) 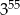 D)
D) 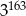
Cena jednego bitcoina wzrosła w stosunku do ceny jednego bitcoina z dnia 1 stycznia 2017 o 1000% i wynosiła w grudniu 2017 roku 46860 zł. Jaka była cena jednego bitcoina w pierwszym dniu 2017 roku?
A) 4686 zł B) 527 zł C) 4260 zł D) 468 zł
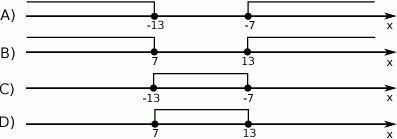
Wskaż rysunek, na którym jest przedstawiony zbiór wszystkich liczb  spełniających warunek:
spełniających warunek: 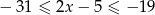 .
.
Wartość wyrażenia 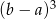 dla
dla 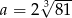 i
i 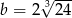 jest równa
jest równa
A) 216 B) 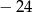 C)
C) 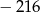 D) 24
D) 24
Funkcją malejącą jest funkcja
A) 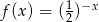 B)
B) 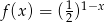 C)
C) 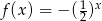 D)
D) 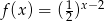
Równanie 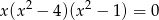 z niewiadomą
z niewiadomą 
A) nie ma rozwiązań w zbiorze liczb rzeczywistych.
B) ma dokładnie dwa rozwiązania w zbiorze liczb rzeczywistych.
C) ma dokładnie trzy rozwiązania w zbiorze liczb rzeczywistych.
D) ma dokładnie pięć rozwiązań w zbiorze liczb rzeczywistych.
Układ równań 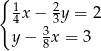
A) nie ma rozwiązań.
B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania.
D) ma nieskończenie wiele rozwiązań.
Wyrażenie 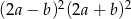 jest równe
jest równe
A) 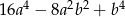 B)
B) 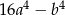 C)
C) 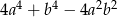 D)
D) 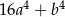
Wierzchołek paraboli o równaniu 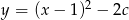 leży na prostej o równaniu
leży na prostej o równaniu 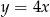 . Wtedy
. Wtedy
A) 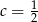 B)
B) 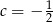 C)
C) 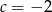 D)
D) 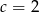
W ciągu geometrycznym 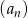 , określonym dla
, określonym dla 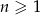 , dane są:
, dane są: 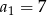 ,
, 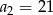 . Wtedy
. Wtedy
A) 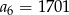 B)
B) 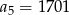 C)
C) 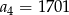 D)
D) 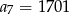
Dwa kolejne wyrazy ciągu arytmetycznego są równe 79 i 75. Wyrazem tego ciągu może być liczba
A) 2015 B) 2016 C) 2017 D) 2018
Dany jest prostokąt 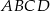 o wierzchołkach
o wierzchołkach 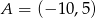 ,
, 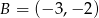 ,
, 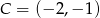 i
i 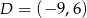 . Który z podanych punktów leży na okręgu opisanym na prostokącie
. Który z podanych punktów leży na okręgu opisanym na prostokącie  ?
?
A) 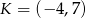 B)
B) 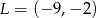 C)
C) 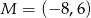 D)
D) 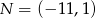
Pole trójkąta przedstawionego na rysunku jest równe
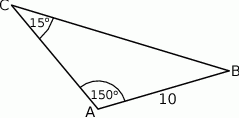
A) 50 B) 25 C) 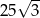 D)
D) 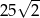
W trójkącie 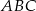 punkt
punkt 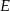 leży na boku
leży na boku 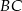 , a punkt
, a punkt 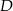 leży na boku
leży na boku 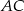 . Odcinek
. Odcinek 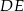 jest równoległy do boku
jest równoległy do boku 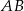 , a ponadto
, a ponadto 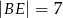 ,
, 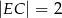 i
i 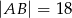 (zobacz rysunek).
(zobacz rysunek).
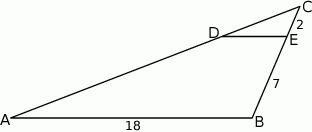
Długość odcinka 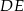 jest równa
jest równa
A) 5 B) 3 C) 6 D) 4
Prosta przechodząca przez punkt 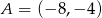 i początek układu współrzędnych jest prostopadła do prostej o równaniu
i początek układu współrzędnych jest prostopadła do prostej o równaniu
A) 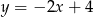 B)
B) 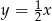 C)
C) 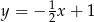 D)
D) 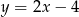
W okręgu o środku 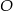 dany jest kąt wpisany
dany jest kąt wpisany 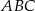 o mierze
o mierze 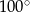
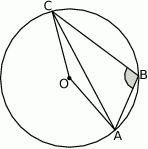
Miara kąta 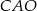 jest równa
jest równa
A) 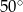 B)
B) 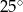 C)
C) 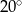 D)
D) 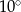
Na rysunku przedstawiono ostrosłup prawidłowy czworokątny 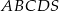 o podstawie
o podstawie 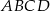 . Odcinek
. Odcinek 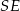 jest wysokością ściany bocznej tego ostrosłupa.
jest wysokością ściany bocznej tego ostrosłupa.
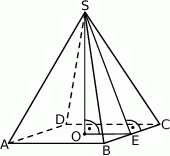
Kąt nachylenia ściany bocznej 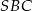 ostrosłupa do płaszczyzny podstawy
ostrosłupa do płaszczyzny podstawy 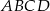 to
to
A) 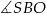 B)
B) 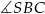 C)
C) 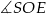 D)
D) 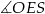
Rzucamy cztery razy symetryczną monetą. Prawdopodobieństwo otrzymania co najmniej jednego orła jest równe
A) 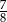 B)
B) 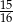 C)
C) 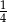 D)
D) 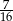
Trójkąt równoboczny o boku długości 6 cm obrócono wokół prostej zawierającej wysokość trójkąta. Objętość powstałej bryły jest równa:
A) 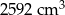 B)
B) 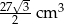 C)
C) 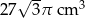 D)
D) 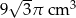
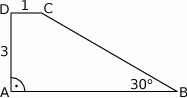
Pole trapezu prostokątnego  przedstawionego na rysunku, jest równe
przedstawionego na rysunku, jest równe
A) 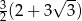 B)
B) 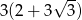 C)
C) 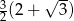 D)
D) 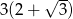
Przekątna graniastosłupa prawidłowego czworokątnego ma długość 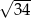 , a krawędź podstawy ma długość 3. Objętość tego graniastosłupa jest równa
, a krawędź podstawy ma długość 3. Objętość tego graniastosłupa jest równa
A) 4 B) 18 C) 36 D) 24
Średnia arytmetyczna cen dziewięciu akcji na giełdzie jest równa 680 zł. Za osiem z tych akcji zapłacono 5500 zł. Cena dziewiątej akcji jest równa
A) 660 zł B) 580 zł C) 620 zł D) 760 zł
W pudełku znajdują się kule w trzech kolorach: czerwone, białe i niebieskie, przy czym prawdopodobieństwo wylosowania kuli czerwonej jest dwa razy mniejsze od prawdopodobieństwa wylosowania kuli białej, a prawdopodobieństwo wylosowania kuli niebieskiej jest trzy razy mniejsze od prawdopodobieństwa wylosowania kuli czerwonej. Prawdopodobieństwo wylosowania kuli białej jest równe
A) 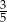 B)
B) 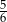 C)
C) 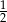 D)
D) 
Zadania otwarte
Jeżeli do licznika i do mianownika nieskracalnego dodatniego ułamka dodamy jego licznik, to otrzymamy 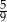 . Wyznacz ten ułamek.
. Wyznacz ten ułamek.
Udowodnij, że dla dowolnych liczb nieujemnych  i
i 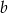 prawdziwa jest nierówność
prawdziwa jest nierówność
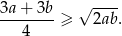
Dany jest trójkąt 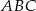 , w którym
, w którym 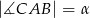 i
i 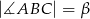 (zobacz rysunek). Na bokach
(zobacz rysunek). Na bokach 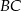 ,
, 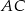 i
i 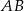 tego trójkąta wybrano odpowiednio punkty
tego trójkąta wybrano odpowiednio punkty 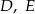 i
i 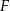 w taki sposób, że
w taki sposób, że 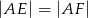 ,
, 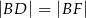 i
i 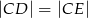 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta 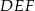 .
.
Suma ośmiu początkowych wyrazów ciągu geometrycznego 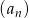 , określonego dla
, określonego dla 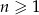 , jest równa 55760. Ponadto
, jest równa 55760. Ponadto 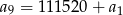 . Oblicz iloraz tego ciągu.
. Oblicz iloraz tego ciągu.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia, że wylosujemy liczbę, która jest równocześnie większa od 40 i podzielna przez 3. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.
Dany jest trójkąt prostokątny 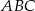 , w którym przyprostokątna
, w którym przyprostokątna 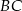 ma długość 6. Punkt
ma długość 6. Punkt 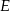 jest środkiem przeciwprostokątnej
jest środkiem przeciwprostokątnej 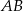 , spodek
, spodek 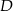 wysokości
wysokości 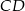 leży między punktami
leży między punktami 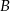 i
i 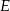 , a odległość między punktami
, a odległość między punktami 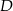 i
i 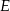 jest równa 7 (zobacz rysunek).
jest równa 7 (zobacz rysunek).
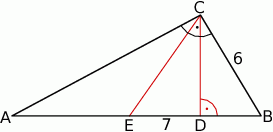
Oblicz obwód trójkąta 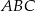 .
.
Ramiona trapezu mają długości 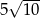 i 20. Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2:3. Oblicz pole tego trapezu.
i 20. Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2:3. Oblicz pole tego trapezu.
Podstawą graniastosłupa prostego 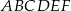 jest trójkąt prostokątny
jest trójkąt prostokątny 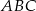 , w którym
, w którym 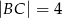 . Promień okręgu opisanego na trójkącie
. Promień okręgu opisanego na trójkącie 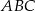 ma długość 3, a sinus kąta nachylenia przekątnej
ma długość 3, a sinus kąta nachylenia przekątnej 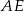 ściany bocznej
ściany bocznej 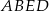 do płaszczyzny podstawy jest równy
do płaszczyzny podstawy jest równy 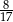 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
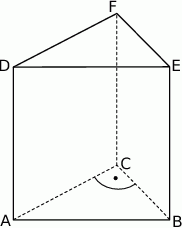
Punkty 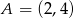 i
i 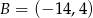 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 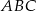 , w którym
, w którym 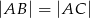 . Wysokość
. Wysokość 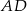 tego trójkąta jest zawarta w prostej o równaniu
tego trójkąta jest zawarta w prostej o równaniu 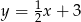 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 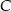 tego trójkąta.
tego trójkąta.

