Zadanie nr 1482488
Na zewnątrz trójkąta prostokątnego 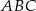 , w którym
, w którym 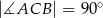 oraz
oraz 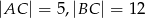 zbudowano kwadrat
zbudowano kwadrat 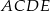 .
.
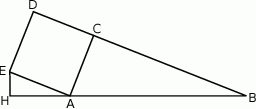
Punkt 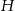 leży na prostej
leży na prostej 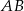 i kąt
i kąt 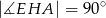 . Oblicz pole trójkąta
. Oblicz pole trójkąta 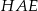 .
.
Rozwiązanie
Najważniejsze w tym zadaniu to zauważyć, że trójkąty prostokątne 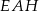 i
i 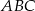 są podobne.
są podobne.
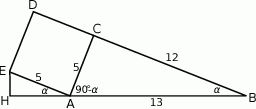
Rzeczywiście, jeżeli oznaczymy 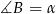 to
to 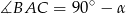 oraz
oraz
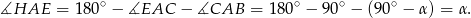
Łatwo też obliczyć skalę podobieństwa tych trójkątów. Z twierdzenia Pitagorasa mamy
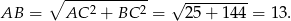
Zatem skala podobieństw jest równa 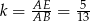 . Ponieważ pole zmienia się jak kwadrat skali podobieństwa, szukane pole trójkąta jest równe
. Ponieważ pole zmienia się jak kwadrat skali podobieństwa, szukane pole trójkąta jest równe
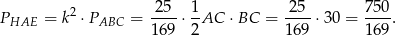
Odpowiedź: