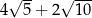Zadanie nr 1818862
W trójkącie prostokątnym równoramiennym 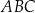 o przeciwprostokątnej
o przeciwprostokątnej 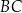 punkt
punkt 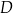 jest środkiem ramienia
jest środkiem ramienia 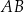 . Odcinek
. Odcinek 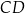 ma długość 5 (zobacz rysunek).
ma długość 5 (zobacz rysunek).
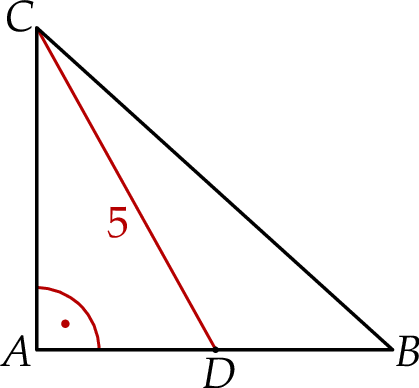
Oblicz obwód trójkąta 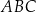 .
.
Rozwiązanie
Trójkąt 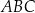 to połówka kwadratu, wiec jeżeli oznaczymy
to połówka kwadratu, wiec jeżeli oznaczymy 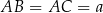 , to
, to
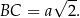
Ponadto,
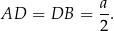
Piszemy twierdzenie Pitagorasa w trójkącie 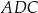 .
.
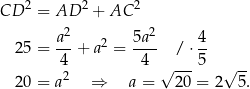
Obwód trójkąta 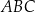 jest więc równy
jest więc równy
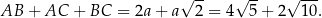
Odpowiedź: