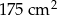/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny

Zadanie nr 2377825

Dodaj do ulubionych
Dodaj do rozwiązanych

Wysokość trójkąta prostokątnego poprowadzona na przeciwprostokątną dzieli ją na odcinki długości 1 cm i 49 cm. Oblicz pole tego trójkąta.

Rozwiązanie

Zaczynamy od schematycznego rysunku.

PIC

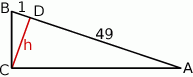
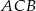Kluczowa w tym zadaniu jest obserwacja, że trójkąty ADC i CDB są podobne do trójkąta ACB (są prostokątne i każdy z nich ma kąt ostry wspólny z ACB ).

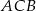Sposób I

Mamy

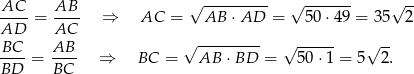
√ --------- √ ------- √ -- AC--= AB-- ⇒ AC = AB ⋅ AD = 50⋅4 9 = 35 2 AD AC BC-- AB-- √ --------- √ ------ √ -- BD = BC ⇒ BC = AB ⋅BD = 5 0⋅1 = 5 2.

Pozostało policzyć pole.

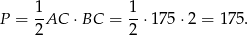
1- 1- P = 2AC ⋅BC = 2 ⋅175 ⋅2 = 175.

Sposób II

Zamiast wyliczać przyprostokątne, wyliczmy długość wysokości 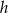h . Jak poprzednio, z podobieństwa, mamy

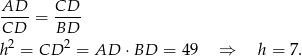
AD-- = CD-- CD BD h2 = CD 2 = AD ⋅ BD = 49 ⇒ h = 7.

Zatem pole jest równe

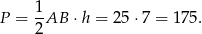
1 P = -AB ⋅h = 25⋅ 7 = 175. 2

 
Odpowiedź: 2 175 cm

Wersja PDF