/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny

Zadanie nr 2823189

Dodaj do ulubionych
Dodaj do rozwiązanych

Na podstawie twierdzenia Pitagorasa można udowodnić bardziej ogólną własność niż ta, o której mówi samo to twierdzenie.

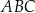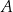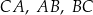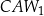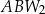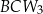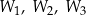Rozważmy trójkąt prostokątny ABC o kącie prostym przy wierzchołku A . Niech każdy z boków tego trójkąta: CA , AB , BC będzie podstawą trójkątów podobnych, odpowiednio: CAW 1 , ABW 2 , BCW 3 . Trójkąty te mają odpowiadające sobie kąty o równych miarach, odpowiednio przy wierzchołkach: W 1, W 2, W 3 .

ZINFO-FIGURE

Pola trójkątów: 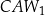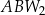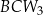CAW 1 , ABW 2 , BCW 3 oznaczymy odpowiednio jako 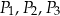P 1,P 2,P3 . Udowodnij, że

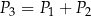
P = P + P 3 1 2

Rozwiązanie

Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Zaloguj się Informacje o abonamencie
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.