Zadanie nr 4757294
Pole prostokąta  jest równe 60, a promień okręgu wpisanego w trójkąt
jest równe 60, a promień okręgu wpisanego w trójkąt  jest równy 2. Oblicz obwód tego prostokąta.
jest równy 2. Oblicz obwód tego prostokąta.
Rozwiązanie
Oznaczmy przez  i
i 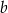 długości boków prostokąta, a
długości boków prostokąta, a  niech będzie długością jego przekątnej.
niech będzie długością jego przekątnej.
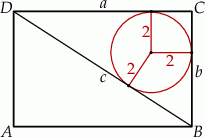
W szczególności
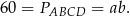
Sposób I
Korzystamy ze wzoru na pole trójkąta z promieniem okręgu wpisanego:
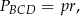
gdzie 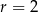 i
i 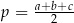 jest połową obwodu. Mamy zatem
jest połową obwodu. Mamy zatem
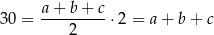
Korzystamy teraz z twierdzenia Pitagorasa.
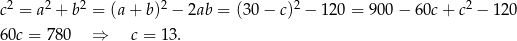
Stąd 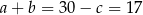 i obwód prostokąta jest równy
i obwód prostokąta jest równy
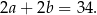
Sposób II
Korzystamy ze wzoru
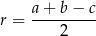
na promień  okręgu wpisanego w trójkąt prostokątny o przyprostokątnych długości
okręgu wpisanego w trójkąt prostokątny o przyprostokątnych długości  i
i 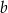 oraz przeciwprostokątnej długości
oraz przeciwprostokątnej długości  . Mamy zatem
. Mamy zatem
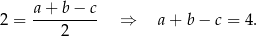
Korzystamy teraz z twierdzenia Pitagorasa.
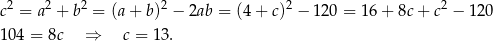
Stąd 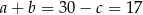 i obwód prostokąta jest równy
i obwód prostokąta jest równy
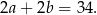
Sposób III
Tym razem nie będziemy korzystać z żadnych wzorów z promieniem okręgu wpisanego – zamiast tego trochę dokładniej popatrzymy na rysunek.
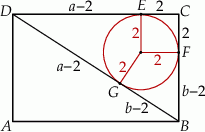
Zauważmy, że jeżeli 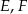 i
i 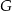 są punktami styczności okręgu wpisanego w trójkąt
są punktami styczności okręgu wpisanego w trójkąt 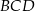 i odpowiednio prostymi
i odpowiednio prostymi 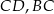 i
i 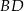 , to
, to 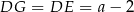 i
i 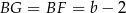 . Zatem na mocy twierdzenia Pitagorasa
. Zatem na mocy twierdzenia Pitagorasa
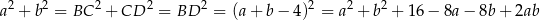
Korzystamy teraz z podanego pola: 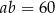 i mamy
i mamy
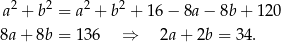
Odpowiedź: 34

