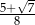Zadanie nr 5452787
W trójkącie prostokątnym stosunek sumy długości przyprostokątnych do długości przeciwprostokątnej jest równy  . Oblicz cosinusy kątów ostrych tego trójkąta.
. Oblicz cosinusy kątów ostrych tego trójkąta.
Rozwiązanie
Szkicujemy trójkąt prostokątny
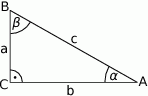
Możemy tak oznaczyć boki trójkąta aby podany warunek zapisać w postaci
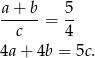
Sposób I
Podnosząc równość 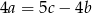 do kwadratu i stosując twierdzenie Pitagorasa mamy
do kwadratu i stosując twierdzenie Pitagorasa mamy
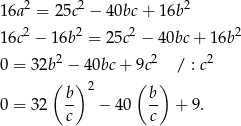
Podstawiając 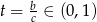 mamy równanie
mamy równanie
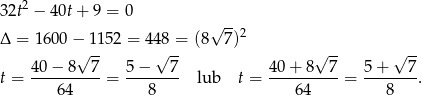
Jeżeli 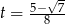 , to
, to
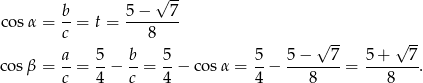
Jeżeli natomiast 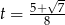 , to otrzymamy te same liczby, ale w odwrotnej kolejności.
, to otrzymamy te same liczby, ale w odwrotnej kolejności.
Sposób II
Tym razem od razu zapiszemy dane równanie z użyciem trygonometrii.
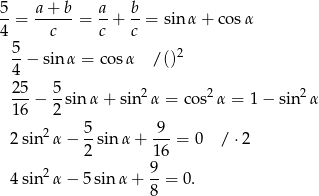
Rozwiązujemy to równanie jak zwykłe równanie kwadratowe
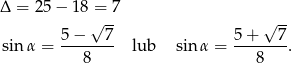
W pierwszym przypadku mamy 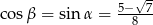 i
i
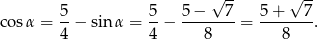
Odpowiedź: 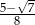 i
i