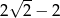Zadanie nr 8351873
Oblicz długość promienia okręgu wpisanego w trójkąt prostokątny, którego kąt ostry ma miarę 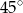 , a długość przeciwprostokątnej jest równa 4.
, a długość przeciwprostokątnej jest równa 4.
Rozwiązanie
Zaczynamy od rysunku
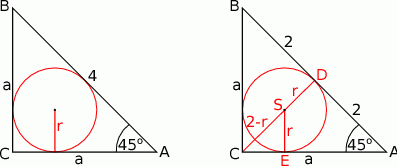
Trójkąt prostokątny z kątem 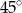 jest równoramienny (jest to połówka kwadratu). Obliczmy długość jego przyprostokątnej.
jest równoramienny (jest to połówka kwadratu). Obliczmy długość jego przyprostokątnej.
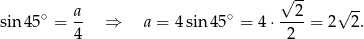
Sposób I
Korzystamy ze wzoru na pole trójkąta z promieniem okręgu wpisanego.
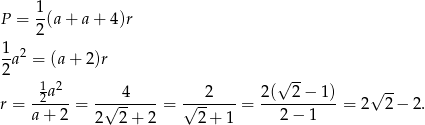
Sposób II
Dorysujmy wysokość 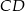 trójkąta
trójkąta 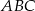 . Trójkąt
. Trójkąt 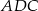 jest ponownie połówką kwadratu, więc
jest ponownie połówką kwadratu, więc 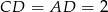 . Stąd
. Stąd 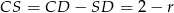 . Patrzymy teraz na trójkąt prostokątny
. Patrzymy teraz na trójkąt prostokątny 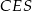 .
.
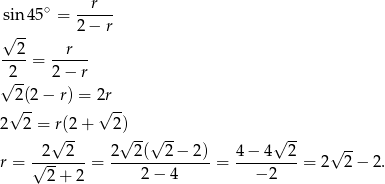
Sposób III
Tak jak poprzednio dorysowujemy wysokość 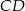 i zauważamy, że trójkąt
i zauważamy, że trójkąt 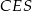 jest połówką kwadratu. Zatem
jest połówką kwadratu. Zatem
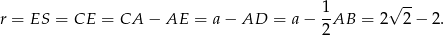
Sposób IV
Korzystamy ze wzoru
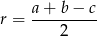
na promień okręgu wpisanego w trójkąt prostokątny o przyprostokątnych długości 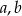 i przeciwprostokątnej długości
i przeciwprostokątnej długości  . W naszej sytuacji mamy
. W naszej sytuacji mamy
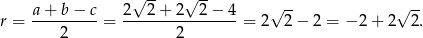
Odpowiedź: