/Gimnazjum/Egzamin gimnazjalny/Egzamin 2018/Próbne testy
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 24 marca 2018 Czas pracy: 90 minut
Wykres przedstawia zależność objętości wody w zbiorniku deszczowym od czasu padania deszczu.
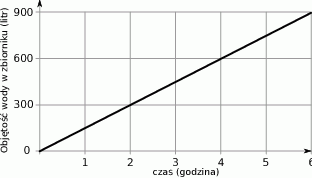
Ile litrów wody przybywa w zbiorniku w czasie 40 minut padania deszczu? Wybierz odpowiedź spośród podanych.
A) 90 litrów B) 100 litrów C) 112,5 litra D) 120 litrów
Kasia przejechała na rowerze trasę długości 900 m w czasie 3 min.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Prędkość średnia, jaką uzyskała Kasia na tej trasie, jest równa
A) 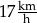 B)
B) 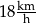 C)
C) 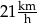 D)
D) 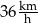
Dane są cztery liczby całkowite: 1258754, 865422, 5418712, 8530236. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wśród podanych liczb są 2 liczby podzielne przez 12. | P | F |
| Wśród podanych liczb są 2 liczby podzielne przez 18. | P | F |
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 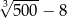 jest dodatnia. jest dodatnia. | P | F |
Liczba 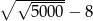 jest ujemna. jest ujemna. | P | F |
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Zaokrąglenie liczby 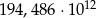 z dokładnością do pełnych setek miliardów jest równe
z dokładnością do pełnych setek miliardów jest równe
A) 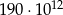 B)
B) 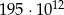 C)
C) 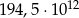 D)
D) 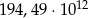
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 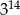 jest 9 razy mniejsza od liczby jest 9 razy mniejsza od liczby 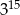 . . | P | F |
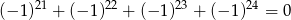 | P | F |
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba  , która spełnia nierówność
, która spełnia nierówność 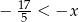
A) może być równa 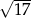 .
.
B) może być równa 3,5.
C) może być równa 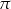 .
.
D) może być dowolną liczbą dodatnią.
Na rysunku przedstawiono sposób ułożenia wzoru z jednakowych elementów i podano długości dwóch fragmentów tego wzoru.
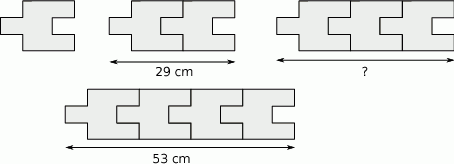
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Fragment wzoru złożony z 3 elementów ma długość
A) 41 cm B) 42 cm C) 45 cm D) 48 cm
W pudełku znajdują się kule w trzech kolorach. Kul niebieskich jest o 30 więcej niż kul zielonych, a kul czerwonych jest o 70 więcej niż kul niebieskich. Kule zielone i czerwone stanowią 75% wszystkich kul znajdujących się w pudełku. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W pudełku jest cztery razy więcej kul niebieskich niż zielonych. | P | F |
| W pudełku jest 40 kul niebieskich. | P | F |
Informacja do zadań 10 i 11
Na loterię przygotowano 500 losów, wśród których jest 40 losów wygrywających. Każdy los wygrywający upoważnia do odbioru nagrody w wysokości 15 zł.
Jak powinna być cena jednego losu, żeby przychód uzyskany ze sprzedaży wszystkich losów był wyższy od sumy wypłaconych nagród o 200 zł? Zaznacz dobrą odpowiedź.
A) 1,2 zł B) 1,6 zł C) 2,6 zł D) 2,5 zł
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Pierwszych 17 losów zakupionych w loterii było przegrywających. Zuzia jako 18 osoba kupuje los w tej loterii. Prawdopodobieństwo, że los Zuzi jest wygrywający jest większe niż 0,08. | P | F |
| W drugiej edycji tej loterii zwiększono liczbę losów wygrywających dwukrotnie, a liczbę losów przegrywających pozostawiono bez zmian. Zatem prawdopodobieństwo wygranej wzrosło w drugiej edycji dwukrotnie. | P | F |
Dana jest kula o objętości 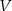 i polu polu powierzchni
i polu polu powierzchni 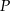 . W tabeli przedstawiono kilka wyrażeń.
. W tabeli przedstawiono kilka wyrażeń.
| Wyrażenie | I | II | III | IV |
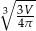 | 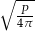 | 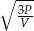 | 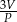 |
Które z tych wyrażeń nie jest równe promieniowi danej kuli? Wybierz właściwą odpowiedź spośród podanych.
A) Wyrażenie I B) Wyrażenie II C) Wyrażenie III D) Wyrażenie IV
Dokończ zdanie. Wybierz odpowiedź spośród podanych
Wyrażenie 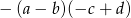 jest równe wyrażeniu
jest równe wyrażeniu
A) 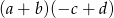 B)
B) 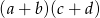 C)
C) 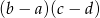 D)
D) 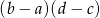
Z prostokąta 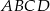 o polu 28 wycięto trójkąt
o polu 28 wycięto trójkąt 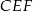 , przy czym punkty
, przy czym punkty 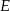 i
i 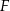 są środkami odpowiednio boków
są środkami odpowiednio boków 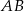 i
i  .
.
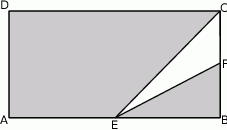
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Pole zacieniowanej figury jest równe
A) 3,5 B) 21 C) 25 D) 24,5
Trójkąt równoboczny rozcięto na 16 przystających trójkątów (rysunek I). Z otrzymanych trójkątów ułożono dwa sześciokąty i mniejszy trójkąt równoboczny (rysunek II).
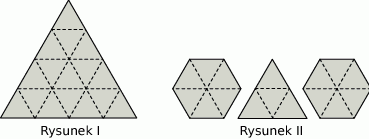
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Obwód dużego trójkąta z rysunku I jest równy sumie obwodów figur na rysunku II. | P | F |
| Suma pól sześciokątów z rysunku II stanowi 75% pola dużego trójkąta z rysunku I. | P | F |
Dwie przecinające się proste utworzyły cztery kąty. Suma miar trzech z tych kątów jest równa 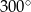 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Suma miar kątów ostrych wyznaczonych przez te proste jest równa 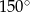 . . | P | F |
| Jeden z dwóch kątów przyległych jest dwa razy większy od drugiego kąta. | P | F |
Czworokąt 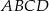 jest deltoidem, w którym dłuższa przekątna
jest deltoidem, w którym dłuższa przekątna 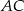 ma taką samą długość jak ramiona
ma taką samą długość jak ramiona 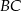 i
i 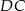 , a kąt
, a kąt 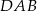 ma miarę
ma miarę 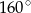 .
.
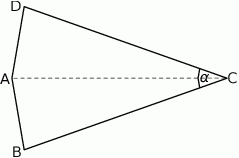
Dokończ poniższe zdanie, wybierając odpowiedź spośród podanych.
Miara kąta 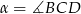 jest równa
jest równa
A) 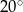 B)
B) 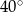 C)
C) 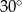 D)
D) 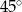
Zbiornik w kształcie odwróconego stożka jest napełniany wodą przy pomocy pompy pracującej ze stałą wydajnością. Napełnienie zbiornika do 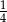 wysokości trwa 15 minut.
wysokości trwa 15 minut.
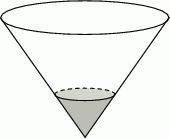
Oceń prawdziwość podanych zdań.
| Napełnienie całego zbiornika trwa 16 godzin. | P | F |
| Napełnienie zbiornika do połowy wysokości trwa 30 minut. | P | F |
Prostokąt o wymiarach 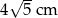 i
i 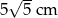 podzielono na 20 jednakowych kwadratów.
podzielono na 20 jednakowych kwadratów.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole jednego kwadratu jest równe
A) 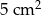 B)
B) 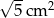 C)
C) 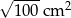 D)
D) 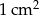
Drewniany sześcian rozcięto na identyczne mniejsze sześciany, a następnie usunięto część z nich tworząc trzy puste tunele łączące przeciwległe ściany (zobacz rysunek). Otrzymana w ten sposób bryła została w całości zanurzona w niebieskiej farbie.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Otrzymana bryła składa się ze 110 małych sześcianów. | P | F |
| 24 małe sześciany mają dokładnie jedną ścianę pomalowaną na niebiesko. | P | F |
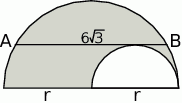
Z półkola o promieniu  wycięto półkole o średnicy
wycięto półkole o średnicy  (zobacz rysunek). Cięciwa
(zobacz rysunek). Cięciwa  jest styczna do mniejszego półkola i jest równoległa do średnicy większego półkola. Oblicz pole zacieniowanego obszaru.
jest styczna do mniejszego półkola i jest równoległa do średnicy większego półkola. Oblicz pole zacieniowanego obszaru.
Do pomalowania 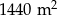 ścian hali magazynowej potrzeba 6 dużych i 2 małych wiader farby, albo 3 dużych i 7 małych wiader farby. Ile co najmniej dużych wiader farby potrzeba do pomalowania ścian tej hali magazynowej? Zapisz obliczenia.
ścian hali magazynowej potrzeba 6 dużych i 2 małych wiader farby, albo 3 dużych i 7 małych wiader farby. Ile co najmniej dużych wiader farby potrzeba do pomalowania ścian tej hali magazynowej? Zapisz obliczenia.
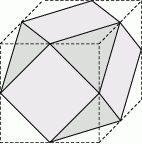
W kostce mającej kształt sześcianu o krawędzi długości 6 ścięto wszystkie naroża płaszczyznami przechodzącymi przez środki odpowiednich krawędzi (zobacz rysunek). Oblicz objętość otrzymanej bryły.