/Gimnazjum/Egzamin gimnazjalny/Egzamin 2018/Próbne testy
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 17 marca 2018 Czas pracy: 90 minut
Adam i Tomek tego samego dnia odbyli górską wycieczkę na Tarnicę. Obaj szli tym samym szlakiem, ale zanim Tomek zdobył szczyt, Adam zaczął już schodzić na dół. Wykresy przedstawiają na jakiej wysokości względem poziomu morza znajdowali się chłopcy – Tomek podczas wejścia na szczyt i Adam podczas zejścia na dół.
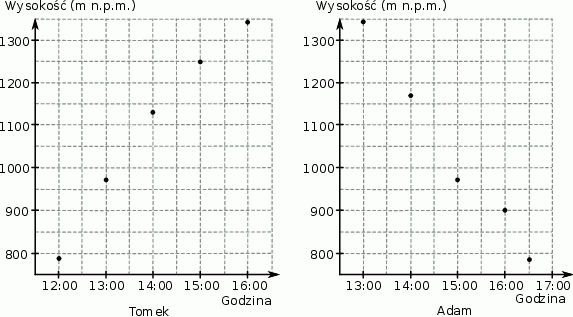
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Chłopcy spotkali się w miejscu położonym między 1000 a 1100 m n.p.m. | P | F |
| Chłopcy spotkali się na szlaku między godziną 14:00 a 15:00. | P | F |
Dwa pojazdy poruszają w tym samym kierunku wokół okrągłego toru o długości 1,8 km. Pojazdy startują w tym samym czasie i pierwszy z nich porusza się z prędkością 15 m/s, a drugi porusza się z prędkością 12 m/s.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pojazdy ponownie spotkają się w miejscu startu po
A) 20 minutach B) 10 minutach C) 1 godzinie D) 30 minutach
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Jeżeli trzecia część liczby przeciwnej do odwrotności sześcianu pewnej liczby jest równa 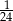 , to ta liczba jest równa
, to ta liczba jest równa
A) 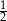 B) 2 C)
B) 2 C) 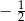 D)
D) 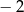
Dane są cztery wyrażenia:

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Największą wartość ma wyrażenie
A) I B) II C) III D) IV
Dana jest liczba dwucyfrowa. W tej liczbie cyfrą dziesiątek jest  , cyfrą jedności jest
, cyfrą jedności jest 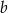 oraz spełnione są warunki:
oraz spełnione są warunki: 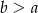 i
i 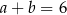 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Warunki zadania spełniają dwie liczby. | P | F |
| Wszystkie liczby spełniające warunki zadania są podzielne przez 6. | P | F |
Liczba 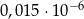 jest równa
jest równa
A) 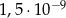 B)
B) 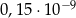 C)
C) 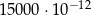 D) 0,0000015
D) 0,0000015
Dane są trzy wyrażenia:
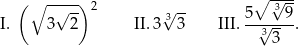
Wartości których wyrażeń są mniejsze od 5? Wybierz właściwą odpowiedź spośród podanych.
A) Tylko I i II. B) Tylko I i III. C) Tylko II i III. D) I, II i III.
Jabłka w trakcie suszenia straciły 40% swojej masy i po wysuszeniu ważą 1,5 kg.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Jabłka przed wysuszeniem ważyły
A) 3,3 kg B) 2,5 kg C) 3 kg D) 2,1 kg
Dane są dwie liczby  i
i  . Wiadomo, że
. Wiadomo, że  oraz
oraz  .
.
![]()
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Najmniejsza możliwa wartość różnicy 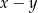 jest równa:
jest równa:
A) 3 B) 9 C) 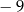 D)
D) 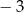
Na rysunku przedstawiono sposób w jaki ustawia się krzesła w pewnej restauracji w zależności od liczby połączonych stołów.
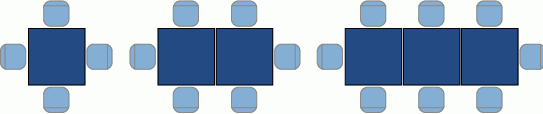
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W układzie z 14 połączonymi stołami jest 30 krzeseł. | P | F |
| Jeżeli podwajamy liczbę stołów w układzie, to liczba krzeseł też rośnie dwukrotnie. | P | F |
Sprzedawca sprzedał w swoim sklepie 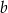 kilogramów bananów i
kilogramów bananów i 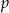 kilogramów pomarańczy: banany sprzedawał po 3,50 zł za kilogram, a pomarańcze po 2,80 zł za kilogram. Na zakup tych warzyw sprzedawca wydał 240 zł. Które wyrażenie przedstawia różnicę kwoty uzyskanej za sprzedane warzywa i kosztu ich zakupu? Wybierz właściwą odpowiedź spośród podanych.
kilogramów pomarańczy: banany sprzedawał po 3,50 zł za kilogram, a pomarańcze po 2,80 zł za kilogram. Na zakup tych warzyw sprzedawca wydał 240 zł. Które wyrażenie przedstawia różnicę kwoty uzyskanej za sprzedane warzywa i kosztu ich zakupu? Wybierz właściwą odpowiedź spośród podanych.
A) 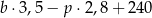 B)
B) 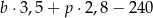
C) 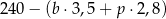 D)
D) 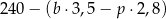
Informacja do zadań 12 i 13
Na diagramie przedstawiono liczbę uczniów z podziałem na płeć w czterech klasach pewnej szkoły.
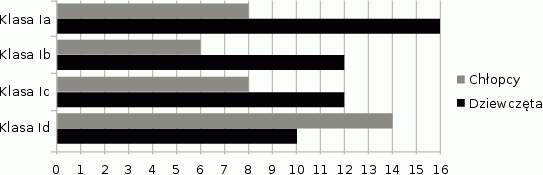
Czy wylosowanie dziewczynki jest bardziej prawdopodobne w klasie Ia, niż w każdej z trzech pozostałych klas? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | w klasie Ia jest więcej dziewcząt, niż w każdej z pozostałych klas. |
| B) | stosunek liczby dziewcząt do liczby chłopców jest największy w klasie Ia. |
| C) | stosunek liczby dziewcząt do liczby chłopców jest taki sam w klasie Ia jak w jednej z pozostałych klas. |
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wylosowania chłopca z klasy Id jest większe niż prawdopodobieństwo wylosowania dziewczynki wśród uczniów uczęszczających do pozostałych klas. | P | F |
Prawdopodobieństwo wylosowania chłopca z klasy Ic jest równe 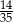 | P | F |
Które z równań jest sprzeczne w zbiorze liczb rzeczywistych? Wybierz odpowiedź spośród podanych.
A) 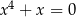 B)
B) 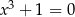 C)
C) 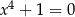 D)
D) 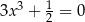
W kwadracie  narysowano dwa półokręgi o średnicach
narysowano dwa półokręgi o średnicach  i
i  (patrz rysunek).
(patrz rysunek).
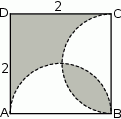
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Pole zacieniowanego obszaru jest równe
A) 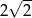 B)
B) 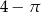 C) 1 D) 2
C) 1 D) 2
Na bokach 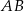 i
i 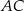 trójkąta prostokątnego
trójkąta prostokątnego 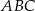 wybrano punkty
wybrano punkty 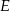 i
i 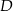 tak, że
tak, że 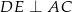 ,
, 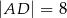 i
i 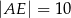 . Przyprostokątna
. Przyprostokątna 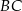 trójkąta
trójkąta 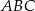 ma długość 18.
ma długość 18.
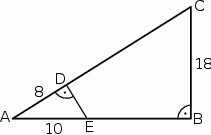
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
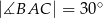 | P | F |
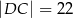 | P | F |
W układzie współrzędnych dane są punkty 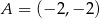 ,
, 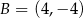 ,
, 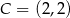 i
i 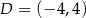 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Czworokąt 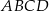 jest trapezem. jest trapezem. | P | F |
Czworokąt  posiada oś symetrii. posiada oś symetrii. | P | F |
Punkty 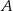 ,
, 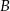 i
i 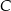 leżą na okręgu o środku
leżą na okręgu o środku 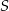 , a prosta
, a prosta 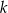 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 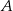 .
.
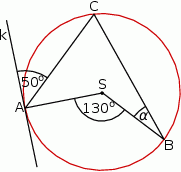
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Zaznaczony na rysunku kąt  zawarty między promieniem
zawarty między promieniem 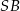 i cięciwą
i cięciwą 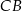 ma miarę
ma miarę
A) 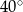 B)
B) 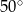 C)
C) 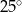 D)
D) 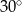
Do akwarium w kształcie prostopadłościanu o wymiarach 80 cm, 50 cm, 30 cm wlano 40 litrów wody. Ile litrów wody należy jeszcze dolać do akwarium, aby sięgała ona do połowy jego wysokości? Wybierz właściwą odpowiedź spośród podanych.
A) 30 B) 20 C) 40 D) 80
Na rysunku przedstawiono siatkę walca.
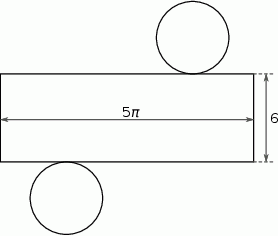
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole powierzchni całkowitej tego walca jest równe
A) 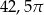 B)
B) 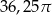 C)
C) 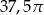 D)
D) 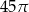
Zapisano dwie różne liczby, których średnia arytmetyczna jest równa 4, oraz trzy inne liczby, których średnia arytmetyczna jest równa 2. Uzasadnij, że średnia arytmetyczna zestawu tych pięciu liczb jest równa 2,8. Zapisz obliczenia.
W trójkącie 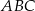 dane są:
dane są: 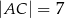 ,
, 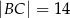 i
i 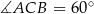 . Oblicz pole trójkąta
. Oblicz pole trójkąta 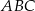 .
.
Na wycieczkę do kina miała pójść grupa 28 uczniów klasy IIb. Ostatecznie jednak liczba osób biorących udział w wycieczce zmniejszyła się o jedną osobę. Stało się tak, gdyż z wycieczki zrezygnowało 25% dziewcząt, oraz do grupy dołączyło kilku chłopców z klasy IIa i liczba chłopców biorących udział w wycieczce zwiększyła się o 25%. Ilu chłopców i ile dziewcząt wzięło udział w wycieczce?
W graniastosłupie prawidłowym sześciokątnym wszystkie krawędzie mają jednakową długość. Oblicz objętość tego graniastosłupa jeżeli jego pole powierzchni całkowitej jest równe 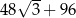 .
.

